
分析 (1)根据奇函数的性质求出x≤0时的解析式,
(2)利用图象变换规律作图;
(3)根据图象直接写答案.
解答 解:(1)当x=0时,f(0)=0,
当x<0时,-x>0,∴f(-x)=($\frac{1}{3}$)-x+1,∴f(x)=-f(-x)=-($\frac{1}{3}$)-x-1=-3x-1.
∴f(x)=$\left\{\begin{array}{l}{(\frac{1}{3})^{x}+1,x>0}\\{0,x=0}\\{-{3}^{x}-1,x<0}\end{array}\right.$.
(2)作出函数图象如图,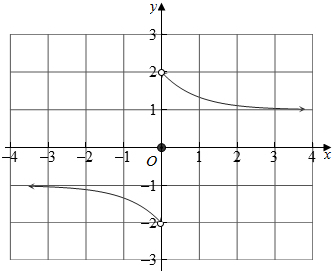
(3)函数f(x)的值域是(-2,-1)∪(1,2)∪{0}.
f(x)的单调减区间是(-∞,0),(0,+∞).
点评 本题考查了奇函数的性质及图象变换,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com