练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    20．某中学举行了一次“环保知识竞赛”活动．为了了解本次竞赛学生成绩情况，从中抽取了部分学生的分数（得分取正整数，满分为100分）作为样本（样本容量为n）进行统计．按照[50，60），[60，70），[70，80），[80，90），[90，100]的分组作出频率分布直方图，并作出样本分数的茎叶图（图中仅列出了得分在[50，60），[90，100]的数据）．

    （Ⅰ）求样本容量n和频率分布直方图中y的值；
    （Ⅱ）在选取的样本中，从竞赛成绩是80分以上（含80分）的同学中随机抽取2名同学到市政广场参加环保知识宣传的志愿者活动，求所抽取的人中至少有一个同学的成绩在[90，100]的概率．

    分析 （Ⅰ）由频率分布直方图和茎叶图能求出样本容量n和频率分布直方图中y的值．
    （Ⅱ）由题意可知，分数在[80，90）有5人，分别为a1，a2，a3，a4，a5，分数在[90，100）有2人，分别为b1，b2，共7人．由此利用列举法能求出所抽取的人中至少有一个同学的成绩在[90，100]的概率．

    解答 解：（Ⅰ）由题意可知：
    样本容量$n=\frac{8}{0.016×10}=50$，
    $y=\frac{2}{50×10}=0.004$．
    （Ⅱ）由题意可知，分数在[80，90）有5人，分别为a1，a2，a3，a4，a5，
    分数在[90，100）有2人，分别为b1，b2，共7人．
    从中抽取2个人共有如下21种方法：
    （a1，a2）（a1，a3）（a1，a4）（a1，a5）（a1，b1）（a1，b2）
    （a2，a3）（a2，a4）（a2，a5）（a2，b1）（a2，b2）（a3，a4）
    （a3，a5）（a3，b1）（a3，b2）（a4，a5）（a4，b1）（a4，b2）
    （a5，b1）（a5，b2）（b1，b2），
    其中至少有一个同学的成绩在[90，100]有11种，
    ∴所求概率为p=$\frac{11}{21}$．

    点评 本题考查样本容量的求法，考查概率的求法，是基础题，解题时要认真审题，注意列举法和频率分布直方图的性质的合理运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    10．已知l，m是两条不同的直线，α，β是两个不同的平面，则以下结论正确的是（　　）
    A．m∥n，m?α，n?β则α∥βB．m∥n，m?α，则n∥α
    C．m∥n，m⊥α，n⊥β，则α∥βD．m⊥n，m?α，则m⊥α

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    11．已知函数f（x）=$\frac{A}{2}$sin（ωx+ϕ）在一个周期内的图象如图，则函数f（x）的解析式为y=2sin（2x+$\frac{2π}{3}$）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．在△ABC中，内角A，B，C的对边分别为a，b，c，已知acos2$\frac{C}{2}$+ccos2$\frac{A}{2}$=$\frac{3}{2}$b．
    （Ⅰ）若b2=ac，判断△ABC的形状．
    （Ⅱ）求cos（A+C）+$\sqrt{3}$sinB的取值范围．．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    15．已知实数x，y满足$\left\{\begin{array}{l}x-2y≥0\\ x+y-3≤0\\ y≥0\end{array}\right.，则（x-2）_{\;}^2+（y+3）_{\;}^2$的最小值为9．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．P为圆锥曲线上一点，F1、F2分别为左、右焦点，|PF1|：|F1F2|：|PF2|=4：3：2，则该圆锥曲线的离心率e=$\frac{1}{2}$或$\frac{3}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．某程序框图如图所示，若该程序运行后输出k的值是6，则输入的整数S0的可能值为（　　）
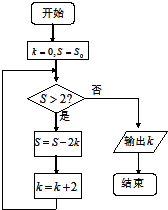
    A．5B．6C．8D．15

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）过点（0，1），离心率为$\frac{{\sqrt{3}}}{2}$，
    （1）求椭圆的标准方程；
    （2）过点（m，0）作圆x2+y2=1的切线l交椭圆G于A，B两点，将|AB|表示为m的函数，并求|AB|的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．给出定义在（0，+∞）上的两个函数f（x）=x2-alnx，g（x）=x-a$\sqrt{x}$．
    （1）若f（x）在x=1处取最值．求实数a的值；
    （2）若函数h（x）=f（x）+g（x2）在区间（0，1]上单调递减，求实数a的取值范围；
    （3）在（1）的条件下，试确定函数m（x）=f（x）-g（x）-6的零点个数，并说明理由．

    查看答案和解析>>

    同步练习册答案