
分析 由平面α∥平面β,且A、C∈α,B、D∈β,直线AB与CD交于点S,根据平面与平面平行的性质定理可得:两条交线应该平行,连接AC、BD,即AC∥BD,则△SAC∽△SBD,又根据相似比的概念及AS=9,BS=8,CD=34,可得:(1)SC=18;(2)SC=306.
解答 解:∵平面α∥平面β,A、C∈α,B、D∈β,直线AB与CD交于点S,
∴根据平面与平面平行的性质定理可得:AC∥BD,
∴△SAC∽△SBD,
(1)$\frac{SC}{SD}=\frac{AS}{SB}$=$\frac{9}{8}$,且SC+SD=CD=34,
则:SC=18;
(2)$\frac{SC}{SD}=\frac{AS}{SB}=\frac{9}{8}$,且SC-SD=CD=34,
则:SC=306.
点评 本题主要考查了空间中直线与平面平行的性质,相似三角形的判定,考查空间想象能力和思维能力,是中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=-2x+1 | B. | y=$\frac{1}{3}$x2+1 | C. | y=-x2-x-1 | D. | y=x2-x+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
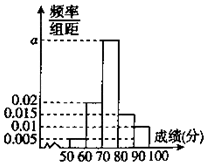 为了了解某学校高二年级学生的物理成绩,从中抽取n名学生的物理成绩(百分制)作为样本,按成绩分成 5组:[50,60),[60,70),[70,80),[80,90),[90,100],频率分布直方图如图所示,成绩落在[70,80)中的人数为20.
为了了解某学校高二年级学生的物理成绩,从中抽取n名学生的物理成绩(百分制)作为样本,按成绩分成 5组:[50,60),[60,70),[70,80),[80,90),[90,100],频率分布直方图如图所示,成绩落在[70,80)中的人数为20.| P(K2≥k) | 0.50 | 0.05 | 0.025 | 0.005 |
| k | 0.455 | 3.841 | 5.024 | 7.879 |
| 男生 | 女生 | 合计 | |
| 优秀 | |||
| 不优秀 | |||
| 合计 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
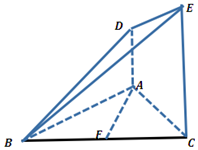 如图,AD⊥平面ABC,CE⊥平面ABC,AC=AD=AB=1,四边形ACED的面积为$\frac{3}{2}$,F为BC的中点,
如图,AD⊥平面ABC,CE⊥平面ABC,AC=AD=AB=1,四边形ACED的面积为$\frac{3}{2}$,F为BC的中点,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,2] | B. | (-1,+∞) | C. | (-1,2] | D. | (-∞,-1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com