
分析 (1)根据双曲线的定义,结合三角形的面积公式建立a,c的方程即可.
(2)设Q(asecθ,$\sqrt{3}$atanθ),根据两角和差的正切公式建立方程公式进行化简证明即可.
解答 解:(1)如图,在△PF1F2中,由余弦定理,
|F1F2|2=|PF1|2+|PF2|2-2|PF1||PF2|cos$\frac{π}{3}$,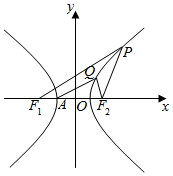 即4c2=(|PF1|-|PF2|)2+2|PF1||PF2|-2|PF1||PF2|cos$\frac{π}{3}$
即4c2=(|PF1|-|PF2|)2+2|PF1||PF2|-2|PF1||PF2|cos$\frac{π}{3}$
=4a2+|PF1||PF2|,
则|PF1||PF2|=4c2-4a2=4b2,
∴△F1PF2的面积S=$\frac{1}{2}$|PF1||PF2|sin$\frac{π}{3}$=$\frac{1}{2}×4{b}^{2}×\frac{\sqrt{3}}{2}$=3$\sqrt{3}$a2.
∴b2=3a2.c=$\sqrt{{a}^{2}+{b}^{2}}$=2a,
则离心率e=$\frac{c}{a}=2$
(2)由(1),双曲线方程为$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{3{a}^{2}}$=1,
若QF2⊥x轴,此时Q(2a,3a),c=2a,△QAF2为等腰Rt△,
∠QAF2=$\frac{1}{2}$QAF2,
下证$λ=\frac{1}{2}$.
令Q(asecθ,$\sqrt{3}$atanθ),
tan∠QF2A=-kQF2=-$\frac{\sqrt{3}atanθ}{asecθ-2a}$=$\frac{\sqrt{3}tanθ}{2-secθ}$,
tan∠QAF2=$\frac{\sqrt{3}atanθ}{asecθ+a}$=$\frac{\sqrt{3}tanθ}{secθ+1}$,
tan2∠QAF2=$\frac{\frac{2\sqrt{3}tanθ}{secθ+1}}{1-(\frac{\sqrt{3}tanθ}{secθ+1})^{2}}$=$\frac{xtacθ(secθ+1)}{(secθ+1)^{2}-3ta{c}^{2}θ}$=$\frac{2\sqrt{3}tacθ(secθ+1)}{-2secθ+2secθ+4}$=$\frac{2\sqrt{3}tanθ(secθ+1)}{-2(secθ+1)(secθ-2)}$=$\frac{\sqrt{3}tanθ}{2-secθ}$=tan∠QF2A,
∴存在常数,使∠QAF2=∠QF2A恒成立.
点评 本题主要考查双曲线离心率的计算,以及三角函数的化简和证明,考查学生的运算能力,综合性较强,难度较大.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:解答题
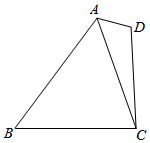 如图,在四边形ABCD中,AB=4,AC=2$\sqrt{3}$,cos∠ACB=$\frac{1}{3}$,∠D=2∠B.
如图,在四边形ABCD中,AB=4,AC=2$\sqrt{3}$,cos∠ACB=$\frac{1}{3}$,∠D=2∠B.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2i | B. | i | C. | -i | D. | -2i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 一年级 | 二年级 | 三年级 | |
| 女生 | 363 | x | y |
| 男生 | 387 | 390 | z |
| A. | 12 | B. | 16 | C. | 18 | D. | 24 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com