
����Ŀ�������������Ժ�������˰�������������ҹ���1980����������������һ�θ�������˰����Ƹ�˰���ĸ�ӭ����ȫ��ʵʩ�Ľ�.2019��1��1��ʵʩ�ĸ�˰������Ҫ���ݰ�������1����˰������Ϊ5000Ԫ����2��ÿ��Ӧ��˰���ö��˰��![]() ����
����![]() ��˰������
��˰������![]() ר��ӿ۳�����3��ר��ӿ۳�����ס������Ů�������������˵�.�¾ɸ�˰������ÿ��Ӧ��˰���ö��˰�����㷽�������Ӧ��˰�ʱ����£�
ר��ӿ۳�����3��ר��ӿ۳�����ס������Ů�������������˵�.�¾ɸ�˰������ÿ��Ӧ��˰���ö��˰�����㷽�������Ӧ��˰�ʱ����£�
�ɸ�˰˰�ʱ�����˰������3500Ԫ�� | �¸�˰˰�ʱ�����˰������5000Ԫ�� | |||
��˰���� | ÿ��Ӧ��˰���ö��˰�� | ˰�ʣ�%�� | ÿ��Ӧ��˰���ö��˰�� | ˰�ʣ�%�� |
1 | ������1500Ԫ�IJ��� | 3 | ������3000Ԫ�IJ��� | 3 |
2 | ����1500Ԫ��4500Ԫ�IJ��� | 10 | ����3000Ԫ��12000Ԫ�IJ��� | 10 |
3 | ����4500Ԫ��9000Ԫ�IJ��� | 20 | ����12000Ԫ��25000Ԫ�IJ��� | 20 |
4 | ����9000Ԫ��35000Ԫ�IJ��� | 25 | ����25000Ԫ��35000Ԫ�IJ��� | 25 |
5 | ����35000Ԫ��55000Ԫ�IJ��� | 30 | ����35000Ԫ��55000Ԫ�IJ��� | 30 |
�� | �� | �� | �� | �� |
�����ȡij��2020��ͬһ����㼶��![]() ��ҵ�ߵ�������ϣ���ͳ�Ʒ�����Ԥ������2019����˾�������24000Ԫ��ͳ�����ϻ����������Ǿ�����ס��ר��۳���ͬʱ������ÿ������ֻ��һ��������Ů�����۳��ĺ��ӣ����������мȲ�������Ů�����۳��ֲ������������˿۳���ֻ������Ů�����۳����������������˿۳���ֻ�����������˿۳�����������Ů�����۳����ȷ�����Ů�����۳��ַ����������˿۳�������֮����
��ҵ�ߵ�������ϣ���ͳ�Ʒ�����Ԥ������2019����˾�������24000Ԫ��ͳ�����ϻ����������Ǿ�����ס��ר��۳���ͬʱ������ÿ������ֻ��һ��������Ů�����۳��ĺ��ӣ����������мȲ�������Ů�����۳��ֲ������������˿۳���ֻ������Ů�����۳����������������˿۳���ֻ�����������˿۳�����������Ů�����۳����ȷ�����Ů�����۳��ַ����������˿۳�������֮����![]() �����⣬���Ǿ�����������ר��ӿ۳����¸�˰�����¸��е�ר��ӿ۳���Ϊ��ס��1000Ԫ/�£���Ů����ÿ��1000Ԫ/�£���������2000Ԫ/�µ�.������и�����㼶��
�����⣬���Ǿ�����������ר��ӿ۳����¸�˰�����¸��е�ר��ӿ۳���Ϊ��ס��1000Ԫ/�£���Ů����ÿ��1000Ԫ/�£���������2000Ԫ/�µ�.������и�����㼶��![]() ��ҵ�߶���������ר��ӿ۳�����Ԥ���ĸ��и�����㼶��
��ҵ�߶���������ר��ӿ۳�����Ԥ���ĸ��и�����㼶��![]() ��ҵ�ߵ��˾���������Ϊ����������룬�����������������˼�룬����������⣺
��ҵ�ߵ��˾���������Ϊ����������룬�����������������˼�룬����������⣺
��1�����ھ������¸�����㼶��![]() ��ҵ��ÿ��Ӧ�ɵĸ�˰��
��ҵ��ÿ��Ӧ�ɵĸ�˰��
��2������и�����㼶��![]() ��ҵ��2019���½ɸ�˰ΪXԪ����X�ķֲ��к�������
��ҵ��2019���½ɸ�˰ΪXԪ����X�ķֲ��к�������
��3�������¾ɸ�˰���������ƴ�2019��1�¿�ʼ���������ٸ��£����и�����㼶��![]() ��ҵ�߸����ٽ��ɵĸ�˰֮�;ͳ���2019����˾������룿
��ҵ�߸����ٽ��ɵĸ�˰֮�;ͳ���2019����˾������룿
���𰸡���1��![]() ����2���ֲ��м�������
����2���ֲ��м�������![]() ����3��11����
����3��11����
��������
��1��������������������¸�����㼶��![]() ��ҵ��ÿ��Ӧ�ɵĸ�˰.
��ҵ��ÿ��Ӧ�ɵĸ�˰.
��2���ֱ�������������ߣ��Ȳ������Ӹ������۳��²������������˿۳�����Ⱥ�½ɸ�˰��ֻ������Ů�����۳����������������˿۳�����Ⱥ�½ɸ�˰��ֻ�����������˿۳�����������Ů�����۳�����Ⱥ�½ɸ�˰���ȷ�����Ů�����۳��ַ����������˿۳�����Ⱥ�½ɸ�˰���ɴ������X�ķֲ��к�![]() .
.
��3�����������¸�������![]() ��ҵ��2019���½ɸ�˰Ϊ1830��������㼶
��ҵ��2019���½ɸ�˰Ϊ1830��������㼶![]() ��ҵ��ÿ�����ٽɽ��ĸ�˰Ϊ2290���з������������11���£�������㼶��
��ҵ��ÿ�����ٽɽ��ĸ�˰Ϊ2290���з������������11���£�������㼶��![]() ��ҵ���ٽɽ��ĸ�˰�ܺ;ͳ���2019���������.
��ҵ���ٽɽ��ĸ�˰�ܺ;ͳ���2019���������.
�⣺��1���������¸�����㼶��![]() ��ҵ��ÿ��Ӧ�ɵĸ�˰Ϊ��
��ҵ��ÿ��Ӧ�ɵĸ�˰Ϊ��
![]() .
.
��2�����������ߣ��Ȳ������Ӹ������۳��²������������˿۳�����Ⱥÿ��Ӧ��˰���ö�Ϊ��
![]() ��
��
�½ɸ�˰![]() ��
��
ֻ������Ů�����۳����������������˿۳�����Ⱥÿ��Ӧ����˰���ö�Ϊ��
![]() ��
��
�½ɸ�˰![]() ��
��
ֻ�����������˿۳�����������Ů�����۳�����Ⱥÿ��Ӧ��˰���ö�Ϊ��
![]() ��
��
�½ɸ�˰![]() ��
��
�ȷ�����Ů�����۳��ַ����������˿۳�����Ⱥÿ��Ӧ��˰���ö�Ϊ��
![]() ��
��
�½ɸ�˰![]() ��
��
��X�ķֲ���Ϊ��
X | 2190 | 1990 | 1790 | 1590 |
P |
|
|
|
|
��![]() .
.
��3�������������¸�������![]() ��ҵ��2019���½ɸ�˰Ϊ1830��
��ҵ��2019���½ɸ�˰Ϊ1830��
�������㼶![]() ��ҵ��ÿ�����ٽɽ��ĸ�˰Ϊ
��ҵ��ÿ�����ٽɽ��ĸ�˰Ϊ![]() ��
��
�辭��x���£�������㼶��![]() ��ҵ���ٽɽ��ĸ�˰���ܺ;ͳ���24000��
��ҵ���ٽɽ��ĸ�˰���ܺ;ͳ���24000��
��![]() ��
��
��![]() ����
����![]() ��
��
�ྭ��11���£�������㼶��![]() ��ҵ���ٽɽ��ĸ�˰�ܺ;ͳ���2019���������.
��ҵ���ٽɽ��ĸ�˰�ܺ;ͳ���2019���������.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������![]() ���������߽���
���������߽���![]() ��ֱ��
��ֱ��![]() �ֱ�������
�ֱ�������![]() ��Բ
��Բ![]() �ڵ�
�ڵ�![]() (���϶���)��
(���϶���)��
��1����֤��![]() Ϊ��ֵ��
Ϊ��ֵ��
��2����![]() ��
��![]() ��
��![]() �ɵȲ����У���ֱ��
�ɵȲ����У���ֱ��![]() �ķ��̣�
�ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2013�껪����ѧ��������֤�����������������һ��������ʽ����������������ϣ��������1900�������23������֮һ������������������������������p��ʹ��p+2��������������(p��p+2)��Ϊ�����������ڲ�����30�������У����ѡȡ������ͬ�����������ܹ�������������ĸ�����
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���ж�һ�����������������̶ȣ���ֵ��![]() �֣��������ϵ��飬��2000λ����μ���ͶƱ����ͳ�ƣ��õ�����Ƶ�ʷֲ�ֱ��ͼ������ͼ����
�֣��������ϵ��飬��2000λ����μ���ͶƱ����ͳ�ƣ��õ�����Ƶ�ʷֲ�ֱ��ͼ������ͼ����

���÷ֲ�����ķ��������в�������ͶƱ�������������ȡ![]() λ�����ٿ���̸�ᣬ��������̶���
λ�����ٿ���̸�ᣬ��������̶���![]() ����5�ˣ�
����5�ˣ�
��1����![]() ��ֵ������д�±���2000λ����ͶƱ�����������ֲ�ͳ�ƣ���
��ֵ������д�±���2000λ����ͶƱ�����������ֲ�ͳ�ƣ���
����̶ȣ������� |
|
|
|
|
|
���� |
��2��������ͶƱ����̶ȵ�ƽ���֣���������ȡ�е�ֵ����
��3��������̶���![]() ��5����ǡ��2λΪŮ�ԣ���̸�Ὣ����5λ��������ѡ��λ���ԣ������Լ�Ů���ұ�ѡ�еĸ��ʣ�
��5����ǡ��2λΪŮ�ԣ���̸�Ὣ����5λ��������ѡ��λ���ԣ������Լ�Ů���ұ�ѡ�еĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����״������һ�����Ͳ������壬��֪�������ð�Լ��ж������ۺ���(MERS)�����ؼ��Ժ����ۺ���(SARS)�Ƚ����ؼ���.����������ں����人������״����(nCoV)����ǰ��δ�������з��ֵĹ�״�����¶���.�˸�Ⱦ������״�����������к�����֢״���ȿ������ٺͺ������ѵ�.�ڽ����ز����У���Ⱦ�ɵ��·������ؼ��Ժ����ۺ�����˥�ߣ���������.ijҽԺΪɸ���״��������Ҫ����ѪҺ�Ƿ�Ϊ���ԣ�����![]() ��ѪҺ���������������ּ��鷽ʽ��
��ѪҺ���������������ּ��鷽ʽ��
��ʽһ����ݼ��飬����Ҫ����n��.
��ʽ������ϼ��飬������![]() ��k��2)��ѪҺ�����ֱ�ȡ�������һ�����.��������Ϊ���ԣ���k�ݵ�ѪҺȫΪ���ԣ������k��ѪҺ����ֻҪ����һ�ξ��ˣ����������Ϊ���ԣ�Ϊ����ȷ��k��ѪҺ�����ļ���Ϊ���ԣ���Ҫ����k������ݼ��飬��ʱ��k��ѪҺ�ļ�������ܹ�Ϊk+1.
��k��2)��ѪҺ�����ֱ�ȡ�������һ�����.��������Ϊ���ԣ���k�ݵ�ѪҺȫΪ���ԣ������k��ѪҺ����ֻҪ����һ�ξ��ˣ����������Ϊ���ԣ�Ϊ����ȷ��k��ѪҺ�����ļ���Ϊ���ԣ���Ҫ����k������ݼ��飬��ʱ��k��ѪҺ�ļ�������ܹ�Ϊk+1.
�����ڽ��ܼ����ѪҺ�����У�ÿ�������ļ����������Ի������Զ��Ƕ����ģ���ÿ�����������Խ���ĸ���Ϊp(0<p<1).��ȡ����![]() ��k��2)��ѪҺ�������Dz�����ݼ��飬��ʽ��������Ҫ������ܴ���Ϊ
��k��2)��ѪҺ�������Dz�����ݼ��飬��ʽ��������Ҫ������ܴ���Ϊ![]() �����û�ϼ��鷽ʽ��������Ҫ������ܴ���Ϊ
�����û�ϼ��鷽ʽ��������Ҫ������ܴ���Ϊ![]() .
.
��1����![]() ������p����k�ĺ�����ϵʽp=f(k).
������p����k�ĺ�����ϵʽp=f(k).
��2����p������ؼ���![]() ��أ�����
��أ�����![]() 2)�Dz�ͬ����ʵ��������x1=1��
2)�Dz�ͬ����ʵ��������x1=1��![]() .
.
(i)��֤������![]() Ϊ�ȱ����У�
Ϊ�ȱ����У�
(ii)��![]() ʱ���û�ϼ��鷽ʽ����ʹ��������Ҫ������ܴ���������ֵ����ݼ�����ܴ���������ֵ���٣���k�����ֵ.
ʱ���û�ϼ��鷽ʽ����ʹ��������Ҫ������ܴ���������ֵ����ݼ�����ܴ���������ֵ���٣���k�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ������ͼ��2020��1��25����2020��2��12������ʡ���������¹ڷ����ۼ�ȷ�ﲡ��������ͼ���������ж���ȷ���ǣ� ��
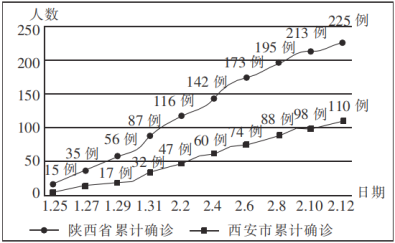
A.1��31������ʡ�¹ڷ����ۼ�ȷ�ﲡ����������ռ�ȳ�����![]()
B.1��25����2��12������ʡ���������¹ڷ����ۼ�ȷ�ﲡ�����ʵ�������
C.2��2�պ�2��10������ʡ�¹ڷ����ۼ�ȷ�ﲡ��������97��
D.2��8�յ�2��10���������¹ڷ����ۼ�ȷ�ﲡ���������ʴ���2��6�յ�2��8�յ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���б����ƣ����Ϸ��Ƽ���ѧ���Ϻ������8�ҵ�λ�������о���ʾ��A��B��O��ABѪ����COVID��19���Դ��ڹ����������������ͳ����ͼ��

�������ϵ������ݣ�������˵��������ǣ� ��
A.���O��Ѫ��ȣ�O��Ѫ��Ⱥ��COVID��19��Բ��У����սϵ�
B.���A��Ѫ��ȣ�A��Ѫ��Ⱥ��COVID��19����У����սϸ�
C.��O��Ѫ��ȣ�B�͡�AB��Ѫ��Ⱥ��COVID��19������Ҫ��
D.��A��Ѫ��ȣ���A��Ѫ��Ⱥ��COVID��19�����У�û�з���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() .
.
��1����![]() ��������
��������![]() �ڵ�
�ڵ�![]() �������߷��̣�
�������߷��̣�
��2������![]() �ĵ������䣻
�ĵ������䣻
��3����![]() ��
��![]() ����ʵ��
����ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ������
������![]() .
.
��1��������![]() �ڵ�
�ڵ�![]() ��������
��������![]() ��ֱ��
��ֱ��![]() ƽ�У���
ƽ�У���![]() �ķ��̣�
�ķ��̣�
��2����![]() ������
������![]() ��
��![]() ��Ϊ����������֤��
��Ϊ����������֤��![]() .
.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com