
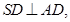 且
且 ,
,
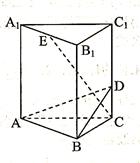
 。(I)求多面体ABCDS的体积;(II)求AD与SB所成角的余弦值;(III)求二面角A—SB—D的余弦值。
。(I)求多面体ABCDS的体积;(II)求AD与SB所成角的余弦值;(III)求二面角A—SB—D的余弦值。
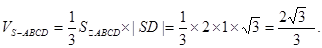 (2)
(2)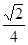 ;(3)
;(3)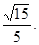
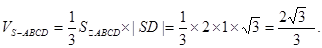
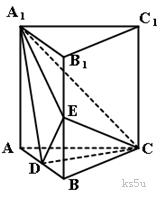
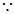 矩形ABCD,
矩形ABCD,
|
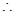 AD//BC,即BC=a,
AD//BC,即BC=a,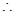 要求AD与SB所成的角,即求BC与SB所成的角在
要求AD与SB所成的角,即求BC与SB所成的角在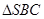 中,由(1)知
中,由(1)知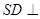 面ABCD。
面ABCD。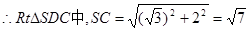
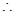 CD是CS在面ABCD内的射影,且
CD是CS在面ABCD内的射影,且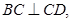
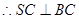
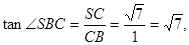
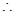 BC与SB所成的角的余弦为
BC与SB所成的角的余弦为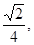
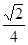
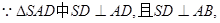
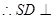 面ABCD。
面ABCD。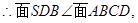 BD为面SDB与面ABCD的交线。
BD为面SDB与面ABCD的交线。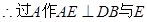
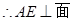 SDB
SDB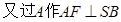 于F,连接EF从而得:
于F,连接EF从而得: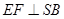
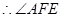 为二面角A—SB—D的平面角
为二面角A—SB—D的平面角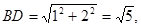
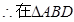 中,
中,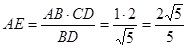
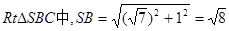
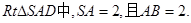
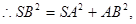
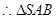 为等腰直角三角形且
为等腰直角三角形且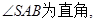
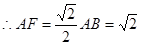
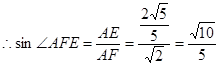 ,
,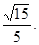


科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
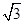 .
.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
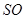 的侧面积为
的侧面积为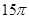 ,底面半径
,底面半径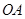 和
和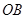 互相垂直,且
互相垂直,且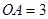 ,
,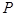 是母线
是母线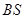 的中点.
的中点.
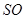 与
与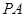 所成角的大小(结果用反三角函数表示).
所成角的大小(结果用反三角函数表示).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com