
 灵星计算小达人系列答案
灵星计算小达人系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
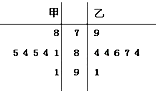 甲、乙两名运动员为了争取得到2016年巴西奥运会的最后一个参赛名额,共进行了7轮比赛,得分情况如茎叶图所示.
甲、乙两名运动员为了争取得到2016年巴西奥运会的最后一个参赛名额,共进行了7轮比赛,得分情况如茎叶图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 概率是频率的稳定值,频率是概率的近似值 | |
| B. | 已知事件M⊆N,则当M发生时,N一定发生 | |
| C. | 若A,B为互斥事件,则P(A)+P(B)<1 | |
| D. | 若一生产厂家称,我们厂生产的产品合格率是0.98,则任取一件该产品,其是合格品的可能性大小为98% |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com