
分析 先求出函数的单调性,再通过讨论m的范围,结合二次函数的性质从而求出m的范围即可.
解答 解:对任意x1,x2∈[-2,+∞)满足$\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}$<0,
得f(x)在[-2,+∞)单调递减,
当m=0时:f(x)=-2x+3,符合题意,
m≠0时,则m<0,
此时,对称轴x=-$\frac{-2}{2m}$=$\frac{1}{m}$≤-2,
解得:m≥-$\frac{1}{2}$,
故答案为:[-$\frac{1}{2}$,0].
点评 本题考察了二次函数的性质,考察函数的单调性问题,考察分类讨论思想,是一道中档题.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a=b<c | B. | a<b<c | C. | b<a<c | D. | c<a<b |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
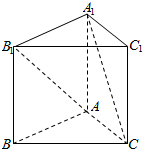 如图,已知正三棱柱ABC-A1B1C1的各条棱长都相等,则异面直线AB1和A1C所成的角的余弦值大小为( )
如图,已知正三棱柱ABC-A1B1C1的各条棱长都相等,则异面直线AB1和A1C所成的角的余弦值大小为( )| A. | $\frac{1}{4}$ | B. | $-\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com