【题目】(12分) 在△ABC中，a、b、c分别为角A、B、C的对边，且
，
（1）求
的度数；
（2）若
， 
，求b和c的值．
【答案】解：（1）由题设得2[1－cos（B＋C）]－（2cos2A－1）＝
，
∵ cos（B＋C）＝－cosA，∴ 2（1＋cosA）－2cos2A＋1＝
，
整理得（2cosA－1）2＝0，∴ cosA＝
，∴ A＝60°．
（2）∵ cosA＝
＝
＝
＝
∴
＝
，∴ bc＝2． 又∵ b＋c＝3，∴ b＝1， c＝2或b＝2， c＝1．
【解析】试题分析：本试题主要是考查了解三角形中边角的转化，以及余弦定理的运用.(1)将已知的条件
，利用倍角进行降幂，得到关于角
的三角方程，从中求解方程即可；(2)由余弦定理得
，将
代入，化简得
，最后联立方程
，求解方程即可得到
的值.
试题解析：（1）由条件
得
∴
即
，也就是
∴
，∵
，∴
(2)由余弦定理得， 
即
，也就是
所以
，又因为
，所以
联立方程
，解得
或
.
科目：高中数学 来源： 题型：
【题目】某中学举办安全法规知识竞赛，从参赛的高一、高二学生中各抽出100人的成绩作为样本，对高一年级的100名学生的成绩进行统计，并按
， 
， 
， 
， 
， 
分组，得到成绩分布的频率分布直方图（如图）。
（1）若规定60分以上（包括60分）为合格，计算高一年级这次竞赛的合格率；
（2）统计方法中，同一组数据常用该组区间的中点值作为代表，据此，估计高一年级这次知识竞赛的学生的平均成绩；
（3）若高二年级这次竞赛的合格率为
，由以上统计数据填写下面
列联表，并问是否有
的把握认为“这次知识竞赛的成绩与年级有关”。
高一 | 高二 | 合计 | |
合格人数 | |||
不合格人数 | |||
合计 |
附：参考数据与公式
高一 | 合计 | ||
合格人数 | a | b | a+b |
不合格人数 | c | d | c+d |
合计 | a+c | b+d | n |
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f(x)＝3ax2＋2bx＋c，a＋b＋c＝0，f(0)>0，f(1)>0，证明a>0，并利用二分法证明方程f(x)＝0在区间[0,1]内有两个实根．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某志愿者到某山区小学支教，为了解留守儿童的幸福感，该志愿者对某班40名学生进行了一次幸福指数的调查问卷，并用茎叶图表示如下（注：图中幸福指数低于70，说明孩子幸福感弱；幸福指数不低于70，说明孩子幸福感强）.
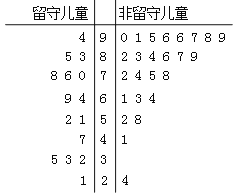
（Ⅰ）根据茎叶图中的数据完成
列联表，并判断能否有
的把握认为孩子的幸福感强与是否是留守儿童有关？
（Ⅱ）从15个留守儿童中按幸福感强弱进行分层抽样，共抽取5人，又在这5人中随机抽取2人进行家访，求这2个学生中恰有一人幸福感强的概率.
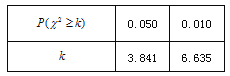
参考公式：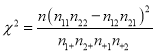 
； 附表：
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设函数f(x)＝ln x－ax(a∈R)(e＝2.718 28…是自然对数的底数)．
(1)判断f(x)的单调性；
(2)当f(x)<0在(0，＋∞)上恒成立时，求a的取值范围；
(3)证明：当x∈(0，＋∞)时，
(1＋x) 
<e.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下列5个命题中正确命题的个数是( )
①对于命题p：x∈R，使得x2＋x＋1<0，则綈p：x∈R，均有x2＋x＋1>0；
②m＝3是直线(m＋3)x＋my－2＝0与直线mx－6y＋5＝0互相垂直的充要条件；
③已知回归直线的斜率的估计值为1.23，样本点的中心为(4,5)，则线性回归方程为
＝1.23x＋0.08；
④若实数x，y∈[－1,1]，则满足x2＋y2≥1的概率为
；
⑤曲线y＝x2与y＝x所围成图形的面积是S＝ (x－x2)dx.
A．2 B．3
C．4 D．5
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某校学生研究性学习小组发现，学生上课的注意力指标随着听课时间的变化而变化，老师讲课开始时，学生的兴趣激增；接下来学生的兴趣将保持较理想的状态一段时间，随后学生的注意力开始分散．设 
表示学生注意力指标，该小组发现 
随时间 
（分钟）的变化规律（
越大，表明学生的注意力越集中）如下： 
（
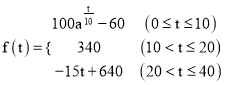，且 
）
若上课后第 
分钟时的注意力指标为 
，回答下列问题：
（1）求 
的值；
（2）上课后第 
分钟时和下课前 
分钟时比较，哪个时间注意力更集中?并请说明理由．
（3）在一节课中，学生的注意力指标至少达到 
的时间能保持多长?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
