
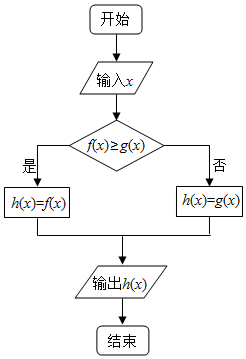
 如图所示的程序框图中,若f(x)=sinx,g(x)=cosx,x∈[0,$\frac{π}{2}$],且h(x)≥m恒成立,则m的最大值是( )
如图所示的程序框图中,若f(x)=sinx,g(x)=cosx,x∈[0,$\frac{π}{2}$],且h(x)≥m恒成立,则m的最大值是( )| A. | 1 | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{1}{2}$ | D. | 0 |
分析 由已知中的程序框图可得该程序的功能是计算并输出分段函数:h(x)=$\left\{\begin{array}{l}{f(x)}&{f(x)≥g(x)}\\{g(x)}&{f(x)<g(x)}\end{array}\right.$的值,分类讨论即可求出h(x)的最小值,可得答案.
解答 解:由已知中的程序框图可得该程序的功能是:
计算并输出分段函数:h(x)=$\left\{\begin{array}{l}{f(x)}&{f(x)≥g(x)}\\{g(x)}&{f(x)<g(x)}\end{array}\right.$的值,
利用正弦函数,余弦函数的图象和性质可知:
当x∈[0,$\frac{π}{4}$)时,f(x)=sinx∈[0,$\frac{\sqrt{2}}{2}$),g(x)=cosx∈($\frac{\sqrt{2}}{2}$,1],g(x)>f(x),
由题意:h(x)=cosx∈($\frac{\sqrt{2}}{2}$,1],
当x∈[$\frac{π}{4}$,$\frac{π}{2}$],f(x)=sinx∈[$\frac{\sqrt{2}}{2}$,1],g(x)=cosx∈[0,$\frac{\sqrt{2}}{2}$],g(x)≤f(x),
由题意:h(x)=sinx∈[$\frac{\sqrt{2}}{2}$,1],
综上,可得x∈[0,$\frac{π}{2}$]时,h(x)的最小值为sin$\frac{π}{4}$=$\frac{\sqrt{2}}{2}$,
又∵h(x)≥m恒成立,
∴m的最大值是$\frac{\sqrt{2}}{2}$,
故选:B.
点评 本题主要考查了程序框图,分段函数的应用,考查了函数恒成立的应用,属于基本知识的考查.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | f(x1)<0,$f({x_2})>-\frac{1}{2}$ | B. | f(x1)<0,$f({x_2})<\frac{1}{2}$ | C. | f(x1)>0,$f({x_2})<-\frac{1}{2}$ | D. | f(x1)>0,$f({x_2})>\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=±$\sqrt{2}$x | B. | y=±2x | C. | y=±$\frac{\sqrt{2}}{2}$x | D. | y=±$\frac{1}{2}$x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
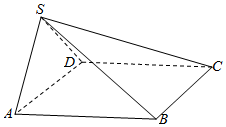 如图所示,在四棱锥S-ABCD中,底面ABCD是正方形,平面SAD⊥平面ABCD,SA=SD=2,AB=3.
如图所示,在四棱锥S-ABCD中,底面ABCD是正方形,平面SAD⊥平面ABCD,SA=SD=2,AB=3.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=±$\frac{4}{3}$x | B. | y=±$\frac{\sqrt{3}}{2}$x | C. | y=±$\frac{9}{16}$x | D. | y=±$\frac{3}{4}$x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知四边形ABCD,ADEF均为平行四边形,DE=BC=2,BD⊥CD,DE⊥平面ABCD.
如图,已知四边形ABCD,ADEF均为平行四边形,DE=BC=2,BD⊥CD,DE⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | 3 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com