Question

11．下表是某地收集到的新房屋的销售价格y（单位：万元）和房屋的面积x（单位：m²）的数据：

x	115	110	80	135	105
y	44.8	41.6	38.4	49.2	42

（1）画出散点图；    
（2）求线性回归方程．

Answer 1

分析 （1）根据表中所给的五对数据，在平面直角坐标系中描出这五个点，得到这组数据的散点图．
（2）根据表中所给的数据，求出横标和纵标的平均数，把求得的数据代入求线性回归方程的系数的公式，利用最小二乘法得到结果，写出线性回归方程

解答 解：（1）散点图如图所示：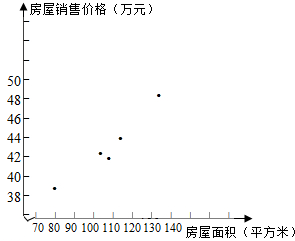

（2）计算$\overline{x}$=$\frac{1}{5}$（115+110+80+135+105）=109，
$\overline{y}$=$\frac{1}{5}$（44.8+41.6+38.4+49.2+42）=43.2，
$\sum_{i=1}^{5}$${{x}_{i}}^{2}$=115²+110²+80²+135²+105²=60975，
$\sum_{i=1}^{5}$（x_iy_i）=115×44.8+110×41.6+80×38.4+135×49.2+105×42=23852；
设所求回归直线方程为$\stackrel{∧}{y}$=bx+a，则b=$\frac{23852-5×109×43.2}{60975-5{×109}^{2}}$≈0.1962，
∴a=$\overline{y}$-b$\overline{x}$≈21.82；
故所求回归直线方程为$\stackrel{∧}{y}$=0.1962x+21.82．

点评 本题考查线性回归方程的求法和应用，解决本题的关键是利用最小二乘法求线性回归方程的系数时，不要弄错数据