
| A. | [$\frac{π}{3}$,$\frac{π}{2}$] | B. | [$\frac{π}{6}$,$\frac{π}{2}$] | C. | [$\frac{π}{6}$,$\frac{π}{3}$] | D. | [$\frac{π}{4}$,$\frac{3π}{8}$] |
分析 由函数的图象平移求得函数g(x)的解析式,进一步求出函数(x)的单调增区间,结合函数g(x)在区间[0,$\frac{a}{3}$]和[2a,$\frac{7π}{6}$]上均单调递增列关于a的不等式组求解.
解答 解:将函数f(x)=2cos2x的图象向右平移$\frac{π}{6}$个单位后得到函数g(x)的图象,
得g(x)=2cos2(x-$\frac{π}{6}$)=2cos(2x-$\frac{π}{3}$),
由$-π+2kπ≤2x-\frac{π}{3}≤2kπ$,得$-\frac{π}{3}+kπ≤x≤\frac{π}{6}+kπ,k∈Z$.
当k=0时,函数的增区间为[$-\frac{π}{3},\frac{π}{6}$],当k=1时,函数的增区间为[$\frac{2π}{3},\frac{7π}{6}$].
要使函数g(x)在区间[0,$\frac{a}{3}$]和[2a,$\frac{7π}{6}$]上均单调递增,
则$\left\{\begin{array}{l}{0<\frac{a}{3}≤\frac{π}{6}}\\{\frac{2π}{3}≤2a<\frac{7π}{6}}\end{array}\right.$,解得a∈[$\frac{π}{3}$,$\frac{π}{2}$].
故选:A.
点评 本题考查三角函数的图象变换,考查了y=Asin(ωx+φ)型函数的性质,是中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
 如图,D、E分别是△ABC的边AB、AC上的点,DE∥BC,且$\frac{AD}{DB}$=2,那么△ADE与四边形DBCE的面积比是$\frac{4}{5}$.
如图,D、E分别是△ABC的边AB、AC上的点,DE∥BC,且$\frac{AD}{DB}$=2,那么△ADE与四边形DBCE的面积比是$\frac{4}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 原点与点(2,3)在直线2x+y-3=0同侧 | B. | 点(3,2)与点(2,3)在直线x-y=0同侧 | ||
| C. | 原点与点(2,1)在直线y-3x+$\frac{1}{2}$=0异侧 | D. | 原点与点(1,4)在直线y-3x+$\frac{1}{2}$=0异侧 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
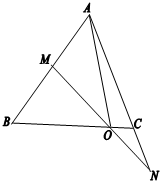 如图所示,在△ABC中,点O是BC上的点,过O的直线MN分别交直线AB,AC于不同的两点M,N,若$\overrightarrow{AB}=2\overrightarrow{AM}$,$\overrightarrow{AC}=\frac{2}{3}\overrightarrow{AN}$,$\overrightarrow{AO}=m\overrightarrow{AB}+n\overrightarrow{AC}$(m>0,n>0),则6m+2n的值为3.
如图所示,在△ABC中,点O是BC上的点,过O的直线MN分别交直线AB,AC于不同的两点M,N,若$\overrightarrow{AB}=2\overrightarrow{AM}$,$\overrightarrow{AC}=\frac{2}{3}\overrightarrow{AN}$,$\overrightarrow{AO}=m\overrightarrow{AB}+n\overrightarrow{AC}$(m>0,n>0),则6m+2n的值为3.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 直线x=$\frac{π}{6}$ | B. | 直线x=$\frac{π}{12}$ | C. | 直线x=-$\frac{π}{6}$ | D. | 直线x=-$\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2sin15°cos15° | B. | 2sin215°-1 | C. | cos215°-sin215° | D. | sin230°+cos230° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com