
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
分析 设现在时间是0,甲乙到场的时间分别是x y,那么就会有0≤x≤60,0≤y≤60,|x-y|如果小于30,就是等待事件,否则不用等待了.由此能求出至少有一辆车需要等待装货物的概率
解答  解:设现在时间是0,甲乙到场的时间分别是x y
解:设现在时间是0,甲乙到场的时间分别是x y
那么就会有:
0≤x≤60,
0≤y≤60,
|x-y|<30,就是等待事件,否则不用等待了.画出来坐标轴如下图
两条斜直线间的面积是等待,
外面的两个三角形面积是不等待,
∴至少有一辆车需要等待装货物的概率p=$\frac{60×60-2×\frac{1}{2}×30×30}{60×60}=\frac{3}{4}$;
故选:D.
点评 本题考查几何概型概率的求法,解题时要认真审题,注意几何概型概率计算公式的合理运用;属于中档题.


科目:高中数学 来源: 题型:解答题
 中央政府为了应对因人口老龄化而造成的劳动力短缺等问题,拟定出台“延迟退休年龄政策”,为了了解人们对“延迟退休年龄政策”的态度,责成人社部进行调研,人社部从网上年龄在15~65岁的人群中随机调查100人,调查数据的频率分布直方图和支持“延迟退休”的人数与年龄的统计结果如下:
中央政府为了应对因人口老龄化而造成的劳动力短缺等问题,拟定出台“延迟退休年龄政策”,为了了解人们对“延迟退休年龄政策”的态度,责成人社部进行调研,人社部从网上年龄在15~65岁的人群中随机调查100人,调查数据的频率分布直方图和支持“延迟退休”的人数与年龄的统计结果如下:| 年龄 | [15,25) | [25,35) | [35,45) | [45,55) | [55,65] |
| 支持“延迟退休”的人数 | 15 | 5 | 15 | 28 | 17 |
| 45岁以下 | 45岁以上 | 总计 | |
| 支持 | |||
| 不支持 | |||
| 总计 |
| P(K2≥k0) | 0.100 | 0.050 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{11}$ | B. | $\frac{1}{12}$ | C. | $\frac{10}{11}$ | D. | $\frac{11}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (0,2) | C. | $({1,\frac{32}{27}}]$ | D. | $({0,\frac{32}{27}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
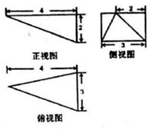 某几何体的三视图如图所示,则该几何体中最长的棱长为( )
某几何体的三视图如图所示,则该几何体中最长的棱长为( )| A. | 3$\sqrt{3}$ | B. | 2$\sqrt{6}$ | C. | $\sqrt{21}$ | D. | 2$\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分条件 | B. | 必要条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com