
 ��������Ϊ��Ӧ�����˿����仯����ɵ��Ͷ�����ȱ�����⣬�ⶨ��̨���ӳ������������ߡ���Ϊ���˽����Ƕԡ��ӳ������������ߡ���̬�ȣ�������粿���е��У����粿������������15��65�����Ⱥ���������100�ˣ��������ݵ�Ƶ�ʷֲ�ֱ��ͼ��֧�֡��ӳ����ݡ��������������ͳ�ƽ�����£�
��������Ϊ��Ӧ�����˿����仯����ɵ��Ͷ�����ȱ�����⣬�ⶨ��̨���ӳ������������ߡ���Ϊ���˽����Ƕԡ��ӳ������������ߡ���̬�ȣ�������粿���е��У����粿������������15��65�����Ⱥ���������100�ˣ��������ݵ�Ƶ�ʷֲ�ֱ��ͼ��֧�֡��ӳ����ݡ��������������ͳ�ƽ�����£�| ���� | [15��25�� | [25��35�� | [35��45�� | [45��55�� | [55��65] |
| ֧�֡��ӳ����ݡ������� | 15 | 5 | 15 | 28 | 17 |
| 45������ | 45������ | �ܼ� | |
| ֧�� | |||
| ��֧�� | |||
| �ܼ� |
| P��K2��k0�� | 0.100 | 0.050 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 6.635 | 10.828 |
���� ��1����ͳ��������д������������۲�ֵ�������ٽ�ֵ�ó����ۣ�
��2������鵽1����45�����µĸ��ʣ�����鵽1����45�����ϵĸ��ʣ��ڸ�������֪X�Ŀ���ȡֵ�������Ӧ�ĸ���ֵ��д���������X�ķֲ��У�������ѧ����ֵ��
��� �⣺��1����ͳ��������2��2���������£�
| 45������ | 45������ | �ܼ� | |
| ֧�� | 35 | 45 | 80 |
| ��֧�� | 15 | 5 | 20 |
| �ܼ� | 50 | 50 | 100 |
| X | 0 | 1 | 2 |
| P | $\frac{15}{28}$ | $\frac{3}{7}$ | $\frac{1}{28}$ |
���� ���⿼������ɢ����������ķֲ�������ѧ�����ļ������⣬Ҳ�����˹ŵ���͵ĸ��ʼ������⣬���е��⣮


 Сѧѧϰ�ð���ϵ�д�
Сѧѧϰ�ð���ϵ�д� Сѧͬ�����������ܾ�ϵ�д�
Сѧͬ�����������ܾ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
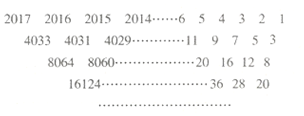 ��������ǡ��ֳơ��������ǡ�������Ϊ����Լ�ڹ�Ԫ1050������ʹ�á��������ǡ����иߴο������㣬������ڹ�Ԫ1261�������ġ��������㷨��һ���У���¼�˼�������������������֮Ϊ������������Դ��ͼ�����������Ĺ���˼·��Դ�ڡ�������ǡ����ñ���������������ɣ��ӵڶ�����ÿһ���е����־������䡰���ϡ�����֮�ͣ��������һ�н���һ��������������ǣ�������
��������ǡ��ֳơ��������ǡ�������Ϊ����Լ�ڹ�Ԫ1050������ʹ�á��������ǡ����иߴο������㣬������ڹ�Ԫ1261�������ġ��������㷨��һ���У���¼�˼�������������������֮Ϊ������������Դ��ͼ�����������Ĺ���˼·��Դ�ڡ�������ǡ����ñ���������������ɣ��ӵڶ�����ÿһ���е����־������䡰���ϡ�����֮�ͣ��������һ�н���һ��������������ǣ�������| A�� | 2017��22016 | B�� | 2018��22015 | C�� | 2017��22015 | D�� | 2018��22016 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-1��4] | B�� | ��2��4] | C�� | ��3��4�� | D�� | {3��4} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ab��ac | B�� | ba��ca | C�� | logab��logac | D�� | $\frac{a}{b}��\frac{a}{c}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-�ޣ�9] | B�� | ��0��9] | C�� | [0��9] | D�� | [0��9�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2$\sqrt{2}$ | B�� | $\sqrt{17}$ | C�� | $\sqrt{15}$ | D�� | 2$\sqrt{5}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ����Ϊ2�е��溯�� | B�� | ����Ϊ2�е�ż���� | ||
| C�� | ����Ϊ�е��溯�� | D�� | ����Ϊ�е�ż���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{4}$ | B�� | $\frac{1}{2}$ | C�� | $\frac{2}{3}$ | D�� | $\frac{3}{4}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com