
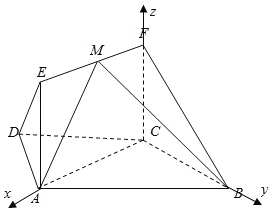
【题目】如图,在梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,四边形
,四边形![]() 为矩形,平面
为矩形,平面![]() 平面
平面![]() ,
,![]() .
.
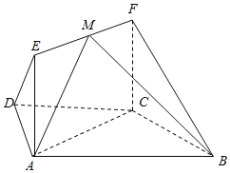
(1)求证:![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使得平面
,使得平面![]() 与平面
与平面![]() 所成锐二面角的平面角为
所成锐二面角的平面角为![]() ,且满足
,且满足![]() ?若不存在,请说明理由;若存在,求出
?若不存在,请说明理由;若存在,求出![]() 的长度.
的长度.
【答案】(1)见解析(2)在线段![]() 上存在点
上存在点![]() 满足题意,
满足题意,![]() .
.
【解析】
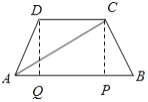
(1)如图所示的等腰梯形![]() 中,经过点
中,经过点![]() ,
,![]() 分别作
分别作![]() ,
,![]() ,垂足为
,垂足为![]() .利用矩形的性质可求出
.利用矩形的性质可求出![]() ,在
,在![]() 中,利用余弦定理可得
中,利用余弦定理可得![]() ,利用勾股定理的逆定理可得
,利用勾股定理的逆定理可得![]() ,再利用面面垂直的性质定理即可证明
,再利用面面垂直的性质定理即可证明![]() 平面
平面![]() ;
;
(2)如图所示,建立空间直角坐标系.设![]() ,设平面
,设平面![]() 的法向量
的法向量![]() ,可得
,可得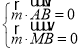 ,取平面
,取平面![]() 的法向量
的法向量![]() ,利用
,利用![]() ,
,![]() ,即可求出.
,即可求出.
(1)如图所示的等腰梯形![]() 中,经过点
中,经过点![]() ,
,![]() 分别作
分别作![]() ,
,![]() ,垂足为
,垂足为![]() ,则
,则![]() 为矩形,
为矩形,![]() .在
.在![]() 中,
中,![]() ,则
,则![]() ,
,
同理可得![]() ,
,![]() .
.
在![]() 中,
中,![]() ,
,
![]() ,
,![]() ,
,![]() .
.
又∵四边形![]() 为矩形,平面
为矩形,平面![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
(2)如图所示,建立空间直角坐标系.
![]() ,
,![]() ,
,![]() ,设
,设![]() ,
,
![]() ,
,
设平面![]() 的法向量
的法向量![]() ,
,
则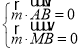 ,∴
,∴ 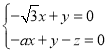
取![]() .
.
取平面![]() 的法向量
的法向量![]() .
.
由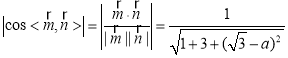 ,
,
由题意可得: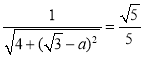 ,
,![]() .
.
解得![]() .
.
因此在线段![]() 上点
上点![]() ,使得平面
,使得平面![]() 与平面
与平面![]() 所成锐二面角的平面角为
所成锐二面角的平面角为![]() ,且满足
,且满足![]() ,
,![]() .
.


科目:高中数学 来源: 题型:
【题目】一项针对都市熟男(三线以上城市,![]() 岁男性)消费水平的调查显示,对于最近一年内是否购买过以下七类高价商品,全体被调查者,以及其中包括的1980年及以后出生(80后)被调查者,1980年以前出生(80前)被调查者回答“是”的比例分别如下:
岁男性)消费水平的调查显示,对于最近一年内是否购买过以下七类高价商品,全体被调查者,以及其中包括的1980年及以后出生(80后)被调查者,1980年以前出生(80前)被调查者回答“是”的比例分别如下:
全体被调查者 | 80后被调查者 | 80前被调查者 | |
电子产品 | 56.9% | 66.0% | 48.5% |
服装 | 23.0% | 24.9% | 21.2% |
手表 | 14.3% | 19.4% | 9.7% |
运动、户外用品 | 10.4% | 11.1% | 9.7% |
珠宝首饰 | 8.6% | 10.8% | 6.5% |
箱包 | 8.1% | 11.3% | 5.1% |
个护与化妆品 | 6.6% | 6.0% | 7.2% |
以上皆无 | 25.3% | 17.9% | 32.1% |
根据表格中数据判断,以下分析错误的是( )
A. 都市熟男购买比例最高的高价商品是电子产品
B. 从整体上看,80后购买高价商品的意愿高于80前
C. 80前超过3成一年内从未购买过表格中七类高价商品
D. 被调查的都市熟男中80后人数与80前人数的比例大约为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() ,
,![]() 为参数,且
为参数,且![]() .
.
(Ⅰ)当![]() 时,判断函数
时,判断函数![]() 是否有极值;
是否有极值;
(Ⅱ)要使函数![]() 的极小值大于零,求参数
的极小值大于零,求参数![]() 的取值范围;
的取值范围;
(Ⅲ)若对(Ⅱ)中所求的取值范围内的任意函数![]() ,函数
,函数![]() 在区间
在区间![]() 内都是增函数,求实数
内都是增函数,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为评估设备![]() 生产某种零件的性能,从设备
生产某种零件的性能,从设备![]() 生产该零件的流水线上随机抽取100个零件为样本,测量其直径后,整理得到下表:
生产该零件的流水线上随机抽取100个零件为样本,测量其直径后,整理得到下表:
直径/mm | 58 | 59 | 61 | 62 | 63 | 64 | 65 | |
件数 | 1 | 1 | 3 | 5 | 6 | 19 | 33 | |
直径/mm | 66 | 67 | 68 | 69 | 70 | 71 | 73 | 合计 |
件数 | 18 | 4 | 4 | 2 | 1 | 2 | 1 | 100 |
经计算,样本的平均值![]() ,标准差
,标准差![]() ,以频率值作为概率的估计值.
,以频率值作为概率的估计值.
(I)为评判一台设备的性能,从该设备加工的零件中任意抽取一件,记其直径为![]() ,并根据以下不等式进行判定(
,并根据以下不等式进行判定(![]() 表示相应事件的概率):①
表示相应事件的概率):①![]() ;②
;②![]() ;③
;③![]() .判定规则为:若同时满足上述三个式子,则设备等级为甲;若仅满足其中两个,则等级为乙;若仅满足其中一个,则等级为丙;若全部都不满足,则等级为丁.试判断设备
.判定规则为:若同时满足上述三个式子,则设备等级为甲;若仅满足其中两个,则等级为乙;若仅满足其中一个,则等级为丙;若全部都不满足,则等级为丁.试判断设备![]() 的性能等级.
的性能等级.
(Ⅱ)将直径尺寸在![]() 之外的零件认定为是“次品”,将直径尺寸在
之外的零件认定为是“次品”,将直径尺寸在![]() 之外的零件认定为“突变品”.从样本的“次品”中随意抽取两件,求至少有一件“突变品”的概率.
之外的零件认定为“突变品”.从样本的“次品”中随意抽取两件,求至少有一件“突变品”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() ,四点
,四点![]() ,
,![]() ,
,![]() ,
,![]() 中恰有三点在椭圆
中恰有三点在椭圆![]() 上.
上.
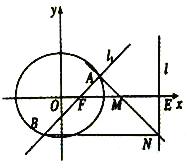
(I)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)过![]() 的右焦点
的右焦点![]() 作斜率为
作斜率为![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,直线
两点,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() 为线段
为线段![]() 的中点,过点
的中点,过点![]() 作直线
作直线![]() 于点
于点![]() .证明:
.证明:![]() ,
,![]() ,
,![]() 三点共线.
三点共线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】赵爽是我国古代数学家、天文学家大约在公元222年赵爽为《周碑算经》一书作序时,介绍了“勾股圆方图”,亦称“赵爽弦图”(以弦为边长得到的正方形是由4个全等的直角三角形再加上中间的一个小正方形组成的)类比“赵爽弦图”,赵爽弦图可类似地构造如图所示的图形,它是由个3全等的等边三角形与中间的一个小等边三角形组成的一个大等边三角形,设DF2AF,若在大等边三角形中随机取一点,则此点取自小等边三角形的概率是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的顶点为原点,其焦点
的顶点为原点,其焦点![]() 到直线
到直线![]() 的距离为
的距离为![]() .设
.设![]() 为直线
为直线![]() 上的点,过点
上的点,过点![]() 作抛物线
作抛物线![]() 的两条切线
的两条切线![]() ,其中
,其中![]() 为切点.
为切点.
(1) 求抛物线![]() 的方程;
的方程;
(2) 当点![]() 为直线
为直线![]() 上的定点时,求直线
上的定点时,求直线![]() 的方程;
的方程;
(3) 当点![]() 在直线
在直线![]() 上移动时,求
上移动时,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln(x2+1)﹣e﹣|x|(e为自然对数的底数),则不等式f(2x+1)>f(x)的解集是( )
A. (﹣1,1)B. (﹣∞,﹣1)∪(1,+∞)
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com