
分析 (1)令n等于1代入2Sn=an2+an中,即可求出首项a1,然后把n换为n-1,得到(an+an-1)(an-an-1-1)=0,即可得出{an}为以a1=1为首项,公差为1的等差数列,再根据b1,b3,b2+10成等差数列,即可求出公比,数列{an}和{bn}的通项公式可求;
(2)求出cn的通项公式,分组求和,利用错位相减求和和裂项求和即可求出.
解答 解:(Ⅰ)2Sn=an2+an,
当n=1时,由2S1=a12+a1,且an>0可得:a1=1,
当n≥2时,2Sn=an2+an…①
2Sn-1=an-12+an-1,…②…(3分)
由 ①-②得:2an=an2+an-an-12-an-1,…②,
即:(an+an-1)(an-an-1-1)=0
∵an>0
∴an-an-1-1=0
∴{an}为以a1=1为首项,公差为1的等差数列,an=n (n∈N*).
由b1=2,2b3=b1+(b2+10),得2q2-q-6=0,解得q=2或$q=-\frac{3}{2}$(舍),
∴${b_n}={b_1}{q^{n-1}}={2^n}$.
(Ⅱ)由(Ⅰ)得${c_n}=n•{2^n}+{(-1)^n}\frac{2n+1}{n(n+1)}=n•{2^n}+{(-1)^n}(\frac{1}{n}+\frac{1}{n+1})$,
∴${T_{2n}}=(1×2+2×{2^2}+…+2n×{2^{2n}})+[{-(1+\frac{1}{2})+(\frac{1}{2}+\frac{1}{3})-(\frac{1}{3}+\frac{1}{4})+…+(\frac{1}{2n}+\frac{1}{2n+1})}]$,
记${W_{2n}}=1×2+2×{2^2}+…+2n×{2^{2n}}$,
则$2{W_{2n}}=1×{2^2}+2×{2^3}+…+2n×{2^{2n+1}}$,
∴$-{W_{2n}}=2+{2^2}+…+{2^{2n}}-2n×{2^{2n+1}}$=$\frac{{2(1-{2^{2n}})}}{1-2}-2n×{2^{2n+1}}$=(1-2n)×22n+1-2,
∴${W_{2n}}=(2n-1)×{2^{2n+1}}+2$,
∴${T_{2n}}={W_{2n}}+(-1+\frac{1}{2n+1})=(2n-1)•{2^{2n+1}}+\frac{1}{2n+1}+1$.
点评 本题考查学生灵活运用数列递推式的求解通项公式,以及错位相减法和裂项求和,属于中档题.


科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
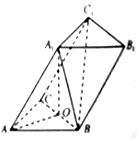 如图,在三棱柱ABC-A1B1C1中,∠BAC=60°,∠A1AC=∠A1AB,AA1=AB=AC=2,点O是BC的中点.
如图,在三棱柱ABC-A1B1C1中,∠BAC=60°,∠A1AC=∠A1AB,AA1=AB=AC=2,点O是BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
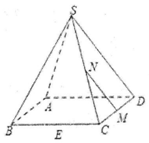 如图,在正四棱锥S-ABCD中,E.M.N分别是BC.CD.SC的中点,动点P的线段MN上运动时,下列四个结论:
如图,在正四棱锥S-ABCD中,E.M.N分别是BC.CD.SC的中点,动点P的线段MN上运动时,下列四个结论:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com