
| A. | x1+x2-1>0 | B. | x1+x2-1<0 | C. | x2-x1>0 | D. | x2-x1<0 |
分析 通过分段化简函数解析式,结合f(x1)=f(x2),作差可得f(x2)-f(1-x1)=f(x1)-f(1-x1).构造函数g(x)=f(x)-f(1-x)(0<x<$\frac{1}{2}$).利用导数可得该函数为定义域上的减函数,得到f(x2)>f(1-x1).再由f(x)=x+$\frac{1}{4x}$在($\frac{1}{2}$,+∞)上为增函数,可得x1+x2-1>0.
解答 解:∵f(x)=e|ln2x|-|x-$\frac{1}{4x}$|=$\left\{\begin{array}{l}{2x-(x-\frac{1}{4x}),x≥\frac{1}{2}}\\{\frac{1}{2x}+(x-\frac{1}{4x}),0<x<\frac{1}{2}}\end{array}\right.$,
∴f(x)=x+$\frac{1}{4x}$(x>0),
∵f(x1)=f(x2)且x1≠x2,
∴不妨设x1<x2,则0<x1<$\frac{1}{2}$<x2.
故1-x1>$\frac{1}{2}$.
∴f(x2)-f(1-x1)=f(x1)-f(1-x1).
设g(x)=f(x)-f(1-x)(0<x<$\frac{1}{2}$).
则g(x)=2x+$\frac{1}{4x}+\frac{1}{4(x-1)}-1$.
g′(x)=$2-\frac{1}{4{x}^{2}}-\frac{1}{4(1-x)^{2}}$<0.
∴g(x)在(0,$\frac{1}{2}$)内为减函数.
得g(x)>g($\frac{1}{2}$)=0,
从而f(x2)-f(1-x1)=f(x1)-f(1-x1)>0.
故f(x2)>f(1-x1).
又f(x)=x+$\frac{1}{4x}$在($\frac{1}{2}$,+∞)上为增函数,
∴x2>1-x1,即x1+x2-1>0.
故选:A.
点评 本题考查函数的零点与方程根的关系,考查数学转化思想方法,训练了利用导数研究函数的单调性,是中档题.


科目:高中数学 来源: 题型:解答题
| 学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 数学偏差x | 20 | 15 | 13 | 3 | 2 | -5 | -10 | -18 |
| 物理偏差y | 6.5 | 3.5 | 3.5 | 1.5 | 0.5 | -0.5 | -2.5 | -3.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$$\overrightarrow{a}$+$\frac{1}{3}$$\overrightarrow{b}$ | B. | -$\frac{1}{3}$$\overrightarrow{a}$+$\frac{1}{3}$$\overrightarrow{b}$ | C. | $\frac{1}{3}$$\overrightarrow{a}$-$\frac{1}{3}$$\overrightarrow{b}$ | D. | -$\frac{1}{3}$$\overrightarrow{a}$-$\frac{1}{3}$$\overrightarrow{b}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
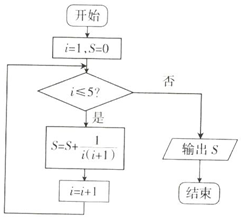
| A. | $\frac{5}{6}$ | B. | $\frac{4}{5}$ | C. | $\frac{6}{7}$ | D. | $\frac{7}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
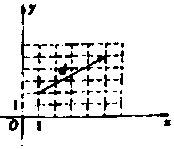
| A. | ?λ>0,使得$\overrightarrow c⊥\overrightarrow d$ | B. | ?λ>0,使得<$\overrightarrow{c}$,$\overrightarrow{d}$>=60° | ||
| C. | ?λ<0,使得<$\overrightarrow{c}$,$\overrightarrow{d}$>=30° | D. | ?λ>0,使得$\overrightarrow c=m\overrightarrow d(m$为不为0的常数) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
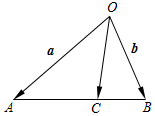 如图,在△OAB中,C是AB上一点,且AC=2CB,设 $\overrightarrow{OA}=\overrightarrow a,\overrightarrow{OB}=\vec b$,则$\overrightarrow{OC}$=$\frac{1}{3}\overrightarrow a+\frac{2}{3}\overrightarrow b$.(用$\overrightarrow a,\overrightarrow b$表示)
如图,在△OAB中,C是AB上一点,且AC=2CB,设 $\overrightarrow{OA}=\overrightarrow a,\overrightarrow{OB}=\vec b$,则$\overrightarrow{OC}$=$\frac{1}{3}\overrightarrow a+\frac{2}{3}\overrightarrow b$.(用$\overrightarrow a,\overrightarrow b$表示)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com