
如图⊙O的半径OB垂直于直径AC,M为AO上一点,BM的延长线交⊙O于点N,过点N的切线交CA的延长线于P
(1)求证: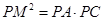
(2)若⊙O的半径为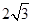 ,OA=
,OA=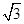 OM,求MN的长
OM,求MN的长
(1)证明见解析;(2)2.
解析试题分析:
解题思路:(1)利用等腰三角形与切割线定理进行证明;(2)利用三角形的相似性进行求解.
规律总结:直线与圆的位置关系,是平面几何问题的常见题型,常考知识由:圆内接四边形、切割线定理、相似三角形、全等三角形等.
试题解析:(1)连结ON,则ON⊥PN,且△OBN为等腰三角形,
则∠OBN=∠ONB,∵∠PMN=∠OMB=900-∠OBN,∠PNM=900-∠ONB
∴∠PMN=∠PNM, ∴PM=PN
由条件,根据切割线定理,有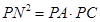
所以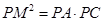
(2)OM=2,在Rt△BOM中,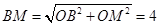
延长BO交⊙O于点D,连接DN
由条件易知△BOM∽△BND,于是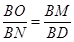
即 ,得BN=6
,得BN=6
所以MN=BN-BM=6-4=2.
考点:1.切割线定理;2.相似三角形.


 学习实践园地系列答案
学习实践园地系列答案科目:高中数学 来源: 题型:填空题
已知圆中两条弦AB与CD相交于点F,E是AB延长线上一点,且DF="CF=√2," AF:FB:BE=4:2:1,若CE与圆相切,则线段CE的长为______.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
扇形AOB中心角为60°,所在圆半径为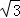 ,它按如下(Ⅰ)(Ⅱ)两种方式有内接矩形CDEF.
,它按如下(Ⅰ)(Ⅱ)两种方式有内接矩形CDEF.
(Ⅰ)矩形CDEF的顶点C、D在扇形的半径OB上,顶点E在圆弧AB上,顶点F在半径OA上,设∠EOB=θ;
(Ⅱ)点M是圆弧AB的中点,矩形CDEF的顶点D、E在圆弧AB上,且关于直线OM对称,顶点C、F分别在半径OB、OA上,设∠EOM= ;
;
试研究(Ⅰ)(Ⅱ)两种方式下矩形面积的最大值,并说明两种方式下哪一种矩形面积最大?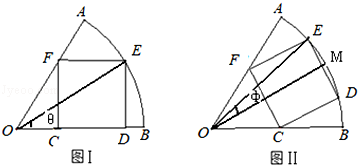
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
如下图所示,在梯形ABCD中,AD∥BC,BD、AC相交于O,过O的直线分别交AB、CD于E、F,且EF∥BC,若AD=12,BC=20,则EF=________.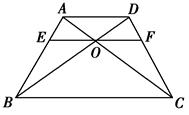
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com