
分析 由题意画出图形,设出A,B坐标分别为 A(2,0),B(2cosα,2sinα),把|$\overrightarrow{OC}$|转化为关于α的三角函数,然后借助于基本不等式求得最值.
解答  解:如图,AB是以O为圆心,半径为2的圆的动弦,
解:如图,AB是以O为圆心,半径为2的圆的动弦,
由$\overrightarrow{AC}•\overrightarrow{BC}$=0,得$\overrightarrow{AC}⊥\overrightarrow{BC}$,∴点C是以AB为直径的圆上的动点(记圆心为D,半径为r),
∴|$\overrightarrow{OC}$|的最大值为:|$\overrightarrow{OD}$|+r=|$\overrightarrow{OD}$|+$\frac{1}{2}$|$\overrightarrow{AB}$|,
以O为原点,OA所在直线为x轴建立直角坐标系,则 A(2,0),
设B(2cosα,2sinα),则D(1+cosα,sinα),
∴|$\overrightarrow{OD}$|+$\frac{1}{2}$|$\overrightarrow{AB}$|=$\sqrt{(1+cosα)^{2}+si{n}^{2}α}+\frac{1}{2}\sqrt{(2cosα-2)^{2}+(2sinα)^{2}}$
=$\sqrt{2+2cosα}+\sqrt{2-2cosα}$$≤\sqrt{2[(\sqrt{2+2cosα})^{2}+(\sqrt{2-2cosα})^{2}}$=$\sqrt{8}=2\sqrt{2}$,
当且仅当2+2cosα=2-2cosα,即cosα=0,也就是$α=\frac{π}{2}$时取最大值,
故答案为:$2\sqrt{2}$.
点评 本题考查平面向量的数量积运算,考查了数形结合的解题思想方法及数学转化思想方法,训练了利用基本不等式求最值,是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
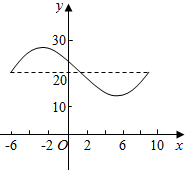 函数y=Asin(ωx+θ)+b的图象如图所示,则此函数的解析式为y=y=10sin($\frac{π}{8}$x+$\frac{3π}{4}$)+20.
函数y=Asin(ωx+θ)+b的图象如图所示,则此函数的解析式为y=y=10sin($\frac{π}{8}$x+$\frac{3π}{4}$)+20.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com