
分析 由对数的运算和和差角的三角函数公式化简可得A=B,可得三角形为等腰三角形.
解答 解:∵在△ABC中lgsinA+lgsinB=2lgcos$\frac{C}{2}$,
∴lgsinAsinB=lgcos2$\frac{C}{2}$,∴sinAsinB=cos2$\frac{C}{2}$,
∴sinAsinB=$\frac{1}{2}$(1+cosC),∴2sinAsinB=1+cosC,
∴2sinAsinB=1-cos(A+B)=1-cosAcosB+sinAsinB,
整理可得sinAsinB+cosAcosB=1即cos(A-B)=1,
∴A-B=0,即A=B,故△ABC为等腰三角形.
故答案为:等腰三角形
点评 本题考查三角函数恒等变换,涉及三角形性质的判定,属基础题.


 灵星计算小达人系列答案
灵星计算小达人系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 150° | B. | 120° | C. | 60° | D. | 30° |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
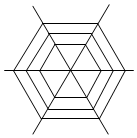 如图是一蜘蛛的辛勤劳动成果,已知该蜘蛛网从内到外由一系列嵌套的正六边形组成,其中最内部的正六边形的边长为a且从内至外正六边形的边长满足数量关系a,2a,3a,4a,…,其中最内部正六边形区域被称为“死亡区域”,只要猎物进入该区域则一定会被捕获,现在有一只蜜蜂飞向该蜘蛛网且其通过该蜘蛛网的最大范围不会超过从内至外的第三个正六边形,则猎物一定会被捕获的概率为$\frac{1}{9}$.
如图是一蜘蛛的辛勤劳动成果,已知该蜘蛛网从内到外由一系列嵌套的正六边形组成,其中最内部的正六边形的边长为a且从内至外正六边形的边长满足数量关系a,2a,3a,4a,…,其中最内部正六边形区域被称为“死亡区域”,只要猎物进入该区域则一定会被捕获,现在有一只蜜蜂飞向该蜘蛛网且其通过该蜘蛛网的最大范围不会超过从内至外的第三个正六边形,则猎物一定会被捕获的概率为$\frac{1}{9}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{0,\frac{π}{6}}]$ | B. | $[{\frac{2π}{3},π}]$ | C. | $[{0,\frac{π}{6}}]$和$[{\frac{π}{3},π}]$ | D. | $[{0,\frac{π}{6}}]$和$[{\frac{2π}{3},π}]$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com