
分析 设出直线l的方程,因为直线l与圆x2+y2-2x+6y+6=0相交,所以圆心到直线l的距离小于半径,用点到直线的距离公式求出圆心到直线l的距离,该距离小于半径,就可得到关于k的不等式,解出k的范围.
解答 解:由题意,点A(-1,-1)在圆外,直线l的斜率存在,设直线l的方程为y+1=k(x+1),即kx-y+k-1=0,
圆x2+y2-2x+6y+6=0可化为(x-1)2+(y+3)2=4,
∵直线l与圆x2+y2-2x+6y+6=0相交,
∴圆心到直线l的距离小于半径
即$\frac{|2k+2|}{\sqrt{{k}^{2}+1}}$<2,解得k<0,
∴直线l的斜率的取值范围为(-∞,0).
点评 本题主要考查直线与圆的位置关系的几何判断方法,若直线与圆相交,则圆心到直线的距离小于半径.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,过抛物线C1:y=$\frac{1}{4}$x2-2的顶点A作两条斜率之积为-$\frac{1}{4}$的直线,与抛物线交于另两点P、Q直线(PQ不与x轴垂直)与椭圆C2:$\frac{{y}^{2}}{4}$+x2=1相交于点M、N.
如图,过抛物线C1:y=$\frac{1}{4}$x2-2的顶点A作两条斜率之积为-$\frac{1}{4}$的直线,与抛物线交于另两点P、Q直线(PQ不与x轴垂直)与椭圆C2:$\frac{{y}^{2}}{4}$+x2=1相交于点M、N.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\sqrt{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1+i | B. | 1-i | C. | 2+i | D. | 2-i |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
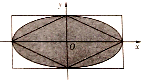 如图,已知矩形长为6,宽为4,在矩形内随机地撒75颗黄豆,数得落在椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{4}$=1外的黄豆数16颗,现随机向椭圆内丢一粒豆子,则豆子落在菱形(菱形顶点为椭圆的顶点)区域内的概率为$\frac{75}{118}$.
如图,已知矩形长为6,宽为4,在矩形内随机地撒75颗黄豆,数得落在椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{4}$=1外的黄豆数16颗,现随机向椭圆内丢一粒豆子,则豆子落在菱形(菱形顶点为椭圆的顶点)区域内的概率为$\frac{75}{118}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com