
【题目】已知倾斜角为![]() 的直线经过抛物线
的直线经过抛物线![]() :
:![]() 的焦点
的焦点![]() ,与抛物线
,与抛物线![]() 相交于
相交于![]() 、
、![]() 两点,且
两点,且![]() .
.
(Ⅰ)求抛物线![]() 的方程;
的方程;
(Ⅱ)过点![]() 的两条直线
的两条直线![]() 、
、![]() 分别交抛物线
分别交抛物线![]() 于点
于点![]() 、
、![]() 和
和![]() 、
、![]() ,线段
,线段![]() 和
和![]() 的中点分别为
的中点分别为![]() 、
、![]() .如果直线
.如果直线![]() 与
与![]() 的倾斜角互余,求证:直线
的倾斜角互余,求证:直线![]() 经过一定点.
经过一定点.
【答案】(Ⅰ)![]() ;(2)
;(2)![]()
【解析】试题分析:
(Ⅰ)设出直线![]() 的方程为
的方程为![]() ,与抛物线方程联立消元后可得
,与抛物线方程联立消元后可得![]() ,结合抛物线的定义及条件可得
,结合抛物线的定义及条件可得![]() ,故抛物线的方程为
,故抛物线的方程为![]() .(Ⅱ)设直线
.(Ⅱ)设直线![]() 的斜率为
的斜率为![]() ,则由条件可得直线
,则由条件可得直线![]() 的斜率为
的斜率为![]() ,由直线
,由直线![]() 与抛物线的交点可得点
与抛物线的交点可得点![]() ,同理点
,同理点![]() ,故
,故![]() ,于是可得直线MN的方程为
,于是可得直线MN的方程为![]() ,可得直线过定点
,可得直线过定点![]() .
.
试题解析:
(Ⅰ)由题意可设直线![]() 的方程为
的方程为![]() ,
,
由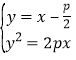 消去y整理得
消去y整理得![]() ,
,
设令![]() ,
,![]() ,
,
则![]() ,
,
由抛物线的定义得![]() ,
,
∴![]() ,
,
∴![]() .
.
∴抛物线的方程为![]() .
.
(Ⅱ)设直线![]() 、
、![]() 的倾斜角分别为
的倾斜角分别为![]() 、
、![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,则
,则![]() .
.
∵直线![]() 与
与![]() 的倾斜角互余,
的倾斜角互余,
∴
![]() ,
,
∴直线![]() 的斜率为
的斜率为![]() .
.
∴直线![]() 的方程为
的方程为![]() ,即
,即![]() ,
,
由![]() 消去x整理得
消去x整理得![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴点![]() ,
,
以![]() 代替点M坐标中的
代替点M坐标中的![]() ,可得点
,可得点![]() ,
,
∴
![]() .
.
∴直线![]() 的方程为
的方程为![]() ,
,
即![]() ,
,
显然当![]() ,
,![]() .
.
∴直线![]() 经过定点
经过定点![]() .
.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:高中数学 来源: 题型:
【题目】某单位决定投资3200元建一仓库(长方体状),高度恒定,它的后墙利用旧墙不花钱,正面用铁栅,每米长造价40元,两侧墙砌砖,每米长造价45元,顶部每平方米造价20元,求:
(1)仓库顶部面积![]() 的最大允许值是多少?
的最大允许值是多少?
(2)为使![]() 达到最大,而实际投资又不超过预算,那么正面铁栅应设计为多长?
达到最大,而实际投资又不超过预算,那么正面铁栅应设计为多长?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校想了解高二数学成绩在学业水平考试中的情况,从中随机抽出![]() 人的数学成绩作为样本并进行统计,频率分布表如下表所示.
人的数学成绩作为样本并进行统计,频率分布表如下表所示.
组号 | 分组 | 频数 | 频率 |
第1组 |
|
|
|
第2组 |
|
|
|
第3组 |
|
|
|
第4组 |
|
|
|
第5组 |
|
|
|
合计 |
|
| |
(1)据此估计这次参加数学考试的高二学生的数学平均成绩;
(2)从这五组中抽取![]() 人进行座谈,若抽取的这
人进行座谈,若抽取的这![]() 人中,恰好有
人中,恰好有![]() 人成绩为
人成绩为![]() 分,
分,![]() 人成绩为
人成绩为![]() 分,
分,![]() 人成绩为
人成绩为![]() 分,
分,![]() 人成绩为
人成绩为![]() 分,求这
分,求这![]() 人数学成绩的方差;
人数学成绩的方差;
(3)从![]() 人的样本中,随机抽取测试成绩在
人的样本中,随机抽取测试成绩在![]() 内的两名学生,设其测试成绩分别为
内的两名学生,设其测试成绩分别为![]() ,
,![]() .
.
(i)求事件“![]() ”的概率;
”的概率;
(ii)求事件“![]() ”的概率.
”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为棱
为棱![]() 的中点,点
的中点,点![]() 为线段
为线段![]() 上一动点.
上一动点.

(Ⅰ)求证:当点![]() 为线段
为线段![]() 的中点时,
的中点时,![]() 平面
平面![]() ;
;
(Ⅱ)设![]() ,试问:是否存在实数
,试问:是否存在实数![]() ,使得平面
,使得平面![]() 与平面
与平面![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]() ?若存在,求出这个实数
?若存在,求出这个实数![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合![]() ,若
,若![]() 是
是![]() 的子集,把
的子集,把![]() 中的所有数的和称为
中的所有数的和称为![]() 的“容量”(规定空集的容量为0),若
的“容量”(规定空集的容量为0),若![]() 的容量为奇(偶)数,则称
的容量为奇(偶)数,则称![]() 为
为![]() 的奇(偶)子集,命题①:
的奇(偶)子集,命题①:![]() 的奇子集与偶子集个数相等;命题②:当
的奇子集与偶子集个数相等;命题②:当![]() 时,
时,![]() 的所有奇子集的容量之和与所有偶子集的容量之和相等,则下列说法正确的是( )
的所有奇子集的容量之和与所有偶子集的容量之和相等,则下列说法正确的是( )
A.命题①和命题②都成立B.命题①和命题②都不成立
C.命题①成立,命题②不成立D.命题①不成立,命题②成立
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国家放开计划生育政策,鼓励一对夫妇生育2个孩子.在某地区的100000对已经生育了一胎夫妇中,进行大数据统计得,有100对第一胎生育的是双胞胎或多胞胎,其余的均为单胞胎.在这99900对恰好生育一孩的夫妇中,男方、女方都愿意生育二孩的有50000对,男方愿意生育二孩女方不愿意生育二孩的有![]() 对,男方不愿意生育二孩女方愿意生育二孩的有
对,男方不愿意生育二孩女方愿意生育二孩的有![]() 对,其余情形有
对,其余情形有![]() 对,且
对,且![]() .现用样本的频率来估计总体的概率.
.现用样本的频率来估计总体的概率.
(1)说明“其余情形”指何种具体情形,并求出![]() ,
,![]() ,
,![]() 的值;
的值;
(2)该地区为进一步鼓励生育二孩,实行贴补政策:凡第一胎生育了一孩的夫妇一次性贴补5000元,第一胎生育了双胞胎或多胞胎的夫妇只有一次性贴补15000元.第一胎已经生育了一孩再生育了二孩的夫妇一次性再贴补20000元.这种补贴政策直接提高了夫妇生育二孩的积极性:原先男方或女方中只有一方愿意生育二孩的夫妇现在都愿意生育二孩,但原先男方、女方都不愿意生育二孩的夫妇仍然不愿意生育二孩.设![]() 为该地区的一对夫妇享受的生育贴补,求
为该地区的一对夫妇享受的生育贴补,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 、
、![]() 的坐标分别是
的坐标分别是![]() ,
,![]() ,直线
,直线![]() ,
,![]() 相交于点
相交于点![]() ,且它们的斜率之积为
,且它们的斜率之积为![]() .
.
(1)求动点![]() 的轨迹方程;
的轨迹方程;
(2)若过点![]() 的直线
的直线![]() 交动点
交动点![]() 的轨迹于
的轨迹于![]() 、
、![]() 两点, 且
两点, 且![]() 为线段
为线段![]() ,
,![]() 的中点,求直线
的中点,求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com