
 如图,已知AA1⊥平面ABC,BB1∥AA1,AB=AC=3,BC=2$\sqrt{5}$,AA1=$\sqrt{7}$,BB1=2$\sqrt{7}$,点E和F分别为BC和A1C的中点.
如图,已知AA1⊥平面ABC,BB1∥AA1,AB=AC=3,BC=2$\sqrt{5}$,AA1=$\sqrt{7}$,BB1=2$\sqrt{7}$,点E和F分别为BC和A1C的中点.分析 (Ⅰ)连接A1B,易证EF∥A1B,由线面平行的判定定理可得;
(Ⅱ)易证AE⊥BC,BB1⊥AE,可证AE⊥平面BCB1,进而可得面面垂直;
(Ⅲ)取BB1中点M和B1C中点N,连接A1M,A1N,NE,易证∠A1B1N即为直线A1B1与平面BCB1所成角,解三角形可得.
解答 (Ⅰ)证明:连接A1B,在△A1BC中,
∵E和F分别是BC和A1C的中点,∴EF∥A1B,
又∵A1B?平面A1B1BA,EF?平面A1B1BA,
∴EF∥平面A1B1BA;
(Ⅱ)证明:∵AB=AC,E为BC中点,∴AE⊥BC,
∵AA1⊥平面ABC,BB1∥AA1,∴BB1⊥平面ABC,
∴BB1⊥AE,又∵BC∩BB1=B,∴AE⊥平面BCB1,
又∵AE?平面AEA1,∴平面AEA1⊥平面BCB1;
(Ⅲ)取BB1中点M和B1C中点N,连接A1M,A1N,NE,
∵N和E分别为B1C和BC的中点,∴NE平行且等于$\frac{1}{2}$B1B,
∴NE平行且等于A1A,∴四边形A1AEN是平行四边形,
∴A1N平行且等于AE,
又∵AE⊥平面BCB1,∴A1N⊥平面BCB1,
∴∠A1B1N即为直线A1B1与平面BCB1所成角,
在△ABC中,可得AE=2,∴A1N=AE=2,
∵BM∥AA1,BM=AA1,∴A1M∥AB且A1M=AB,
又由AB⊥BB1,∴A1M⊥BB1,
在RT△A1MB1中,A1B1=$\sqrt{{B}_{1}{M}^{2}+{A}_{1}{M}^{2}}$=4,
在RT△A1NB1中,sin∠A1B1N=$\frac{{A}_{1}N}{{A}_{1}{B}_{1}}$=$\frac{1}{2}$,
∴∠A1B1N=30°,即直线A1B1与平面BCB1所成角的大小为30°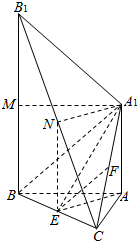
点评 本题考查线面垂直与平行关系的证明,涉及直线与平面所成的角,属中档题.


 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案科目:高中数学 来源: 题型:选择题
| A. | 3,-2 | B. | 3,2 | C. | 3,-3 | D. | -1,4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 7 | B. | 8 | C. | 9 | D. | 14 |
查看答案和解析>>
科目:高中数学 来源:2016-2017学年安徽六安一中高二上文周末检测三数学试卷(解析版) 题型:解答题
已知函数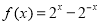 ,数列
,数列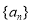 满足
满足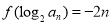 .
.
(1)求数列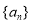 的通项公式;
的通项公式;
(2)证明:数列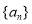 是递减数列.
是递减数列.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com