
已知抛物线 的顶点为原点,其焦点
的顶点为原点,其焦点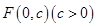 到直线
到直线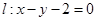 的距离为
的距离为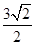 .设
.设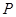 为直线
为直线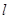 上的点,过点
上的点,过点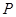 作抛物线
作抛物线 的两条切线
的两条切线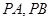 ,其中
,其中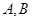 为切点.
为切点.
(Ⅰ)求抛物线 的方程;
的方程;
(Ⅱ)设点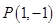 为直线
为直线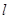 上的点,求直线
上的点,求直线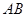 的方程;
的方程;
(Ⅲ) 当点 在直线
在直线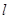 上移动时,求
上移动时,求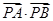 的最小值.
的最小值.
(1) 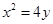 (2)
(2) 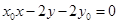 (3)
(3) 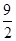
解析试题分析: (1)利用点到直线的距离公式直接求解C的值,便可确定抛物线方程;(2)利用求导的思路确定抛物线的两条切线,借助均过点P,得到直线方程;(3)通过直线与抛物线联立,借助韦达定理将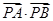 进行转化处理,通过参数的消减得到函数关系式
进行转化处理,通过参数的消减得到函数关系式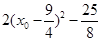 是解题的关键,然后利用二次函数求最值,需注意变量的范围.
是解题的关键,然后利用二次函数求最值,需注意变量的范围.
试题解析:(1)依题意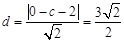 ,解得
,解得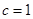 (负根舍去) (2分)
(负根舍去) (2分) 抛物线
抛物线 的方程为
的方程为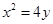 ; (4分)
; (4分)
(2)设点 ,
,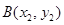 ,由
,由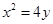 ,即
,即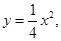 得
得
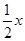 .
.
∴抛物线 在点
在点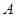 处的切线
处的切线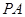 的方程为
的方程为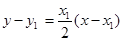 ,即
,即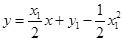 . (5分)
. (5分)
因为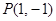 在切线
在切线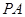 上且
上且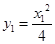 所以
所以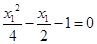 ,
,
从而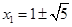 同理,
同理,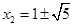 , (6分)
, (6分)
不妨取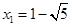 ,
,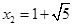 所以
所以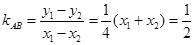 , (7分)
, (7分)
又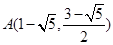 ,∴直线
,∴直线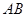 的方程为
的方程为 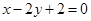 (8分)
(8分)
(3)依据(2)由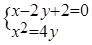 得,
得,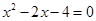 (9分)
(9分)
于是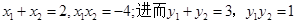 , (10分)
, (10分)
所以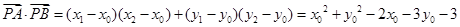
又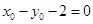 ,所以
,所以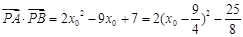 , (11分)
, (11分)
从而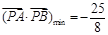 (12分)
(12分)
考点:抛物线的方程、定义、切线方程以及直线与抛物线的位置关系.


科目:高中数学 来源: 题型:解答题
如图所示,已知圆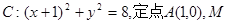 为圆上一动点,点
为圆上一动点,点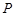 是线段
是线段 的垂直平分线与直线
的垂直平分线与直线 的交点.
的交点.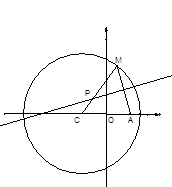
(1)求点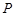 的轨迹曲线
的轨迹曲线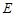 的方程;
的方程;
(2)设点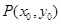 是曲线
是曲线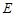 上任意一点,写出曲线
上任意一点,写出曲线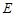 在点
在点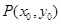 处的切线
处的切线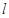 的方程;(不要求证明)
的方程;(不要求证明)
(3)直线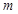 过切点
过切点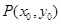 与直线
与直线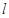 垂直,点
垂直,点 关于直线
关于直线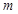 的对称点为
的对称点为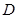 ,证明:直线
,证明:直线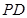 恒过一定点,并求定点的坐标.
恒过一定点,并求定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
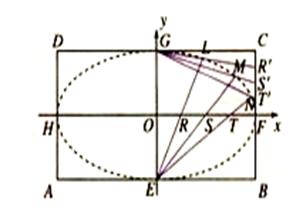
矩形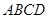 的中心在坐标原点,边
的中心在坐标原点,边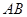 与
与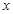 轴平行,
轴平行,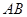 =8,
=8,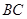 =6.
=6.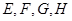 分别是矩形四条边的中点,
分别是矩形四条边的中点,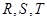 是线段
是线段 的四等分点,
的四等分点,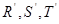 是线段
是线段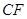 的四等分点.设直线
的四等分点.设直线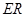 与
与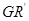 ,
,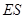 与
与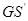 ,
,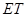 与
与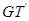 的交点依次为
的交点依次为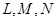 .
.
(1)以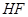 为长轴,以
为长轴,以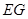 为短轴的椭圆Q的方程;
为短轴的椭圆Q的方程;
(2)根据条件可判定点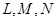 都在(1)中的椭圆Q上,请以点L为例,给出证明(即证明点L在椭圆Q上).
都在(1)中的椭圆Q上,请以点L为例,给出证明(即证明点L在椭圆Q上).
(3)设线段 的
的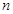 (
(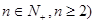 等分点从左向右依次为
等分点从左向右依次为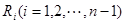 ,线段
,线段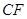 的
的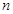 等分点从上向下依次为
等分点从上向下依次为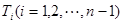 ,那么直线
,那么直线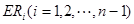 与哪条直线的交点一定在椭圆Q上?(写出结果即可,此问不要求证明)
与哪条直线的交点一定在椭圆Q上?(写出结果即可,此问不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,F1,F2分别是椭圆C: +
+ =1(a>b>0)的左、右焦点,A是椭圆C的顶点,B是直线AF2与椭圆C的另一个交点,∠F1AF2=60°
=1(a>b>0)的左、右焦点,A是椭圆C的顶点,B是直线AF2与椭圆C的另一个交点,∠F1AF2=60°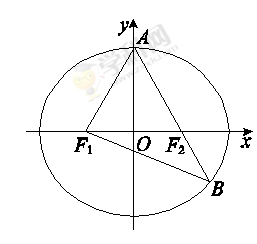
(1)求椭圆C的离心率;
(2)已知△AF1B的面积为40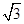 ,求a,b的值
,求a,b的值
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,斜率为 的直线过抛物线
的直线过抛物线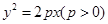 的焦点,与抛物线交于两点A、B, M为抛物线弧AB上的动点.
的焦点,与抛物线交于两点A、B, M为抛物线弧AB上的动点.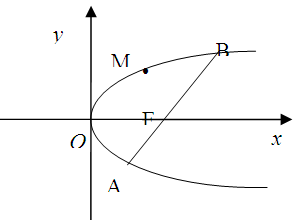
(Ⅰ).若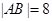 ,求抛物线的方程;
,求抛物线的方程;
(Ⅱ).求△ABM面积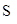 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在直角坐标系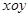 上取两个定点
上取两个定点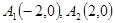 ,再取两个动点
,再取两个动点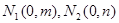 且
且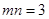 .
.
(I)求直线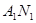 与
与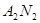 交点的轨迹
交点的轨迹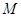 的方程;
的方程;
(II)已知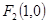 ,设直线:
,设直线: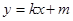 与(I)中的轨迹
与(I)中的轨迹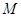 交于
交于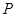 、
、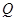 两点,直线
两点,直线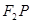 、
、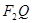 的倾斜角分别为
的倾斜角分别为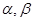 且
且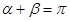 ,求证:直线过定点,并求该定点的坐标.
,求证:直线过定点,并求该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某跳水运动员在一次跳水训练时的跳水曲线为如图所示的抛物线一段,已知跳水板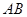 长为2m,跳水板距水面
长为2m,跳水板距水面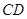 的高
的高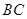 为3m,
为3m, =5m,
=5m,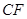 =6m,为安全和空中姿态优美,训练时跳水曲线应在离起跳点
=6m,为安全和空中姿态优美,训练时跳水曲线应在离起跳点 m(
m(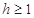 )时达到距水面最大高度4m,规定:以
)时达到距水面最大高度4m,规定:以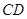 为横轴,
为横轴, 为纵轴建立直角坐标系.
为纵轴建立直角坐标系.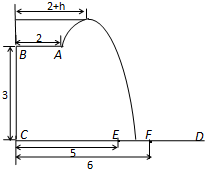
(1)当 =1时,求跳水曲线所在的抛物线方程;
=1时,求跳水曲线所在的抛物线方程;
(2)若跳水运动员在区域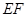 内入水时才能达到压水花的训练要求,求达到压水花的训练要求时
内入水时才能达到压水花的训练要求,求达到压水花的训练要求时 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com