
分析 (1)令x=cosα,y=1+sinα,α∈[0,2π),由三角函数的性质能求出2x+y的范围.
(2)由已知c≥-x-y恒成立,由-x-y=-sinα-cosα-1=-$\sqrt{2}$sin(α+$\frac{π}{4}$)-1,能求出c的范围.
(3)由$\frac{y-2}{x+2}$=$\frac{sinα-1}{cosα+2}$,得$\frac{y-2}{x+2}$的取值范围是单位圆x2+y2=1上一点和点(-2,1)连线的斜率k的取值范围,由点到直线距离公式能求出$\frac{y-2}{x+2}$的取值范围.
(4)(x+1)2+(y+2)2=cos2α+(1+sinα)2+2cosα+4(1+sinα)+5,由此利用三角函数能求出(x+1)2+(y+2)2的取值范围.
解答 解:(1)∵P是圆x2+y2-2y=0上的动点,∴P是圆x2+(y-1)2=1上的动点,圆的圆心是(0,1),半径r=1.
则圆的参数成为$\left\{\begin{array}{l}{x=cosα}\\{y=1+sinα}\end{array}\right.$,α∈[0,2π),
∴2x+y=sinα+2cosα+1=$\sqrt{5}$sin(α+β)+1,
∴2x+y的范围是[1-$\sqrt{5}$,1+$\sqrt{5}$].
(2)∵x+y+c≥0恒成立,∴c≥-x-y恒成立
∵-x-y=-sinα-cosα-1=-$\sqrt{2}$sin(α+$\frac{π}{4}$)-1
∴-x-y的最大值为$\sqrt{2}$-1,
∴c的范围是($\sqrt{2}-1$,+∞).
(3)∵$\frac{y-2}{x+2}$=$\frac{1+sinα-2}{cosα+2}$=$\frac{sinα-1}{cosα+2}$,代表点(cosα,sinα)与(-2,1)连线的斜率,
∴$\frac{y-2}{x+2}$的取值范围是单位圆x2+y2=1上一点和点(-2,1)连线的斜率k的取值范围,
点(-2,1)是定点,(cosα,sinα)在圆x2+y2=1上运动,
∴点(cosα,sinα)与(-2,1)连线与圆相切时(共两个情况)分别取得最大值与最小值,
设点(cosα,sinα)与(-2,1)连线l的方程为y-1=k(x+2),即kx-y+2k+1=0,
∵l与圆相切,∴原点(0,0)到直线l的距离为1,
由点到直线距离公式,得:|$\frac{k×0-0+2k+1}{\sqrt{{k}^{2}+1}}$|=1,
整理,得3k2-4k=0,解得k=0或k=-$\frac{4}{3}$.
∴$\frac{y-2}{x+2}$的取值范围是[-$\frac{4}{3}$,0].
(4)(x+1)2+(y+2)2=x2+2x+1+y2+4y+4
=cos2α+(1+sinα)2+2cosα+4(1+sinα)+5
=cos2α+sin2α+6sinα+2cosα+10
=2$\sqrt{10}$sin(α+θ)+11,
∴(x+1)2+(y+2)2的取值范围是[11-2$\sqrt{10}$,11+2$\sqrt{10}$].
点评 本题考查代数式的取值范围的求法,是中档题,解题时要注意圆的方程、三角函数、点到直线距离公式、等价转化思想的合理运用.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | 2$\sqrt{3}$ | C. | $\frac{2}{3}$$\sqrt{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
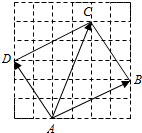
| A. | -$\frac{\sqrt{5}}{5}$ | B. | -$\frac{8\sqrt{5}}{5}$ | C. | $\frac{8\sqrt{5}}{5}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com