
分析 设出顶点O到底面中心o1的距离,再求底面边长和底面面积,求出体积表达式,利用导数求出高为何时体积取得最大值.
解答 解:设帐篷的顶点O到底面中心O1的距离为h(1<h<4),
则帐篷底面正方形的对角线长为a=2$\sqrt{3-(h-1)^{2}}$=2$\sqrt{8-{h}^{2}+2h}$.
∴底面正方形的面积S=$\frac{1}{2}{a}^{2}$=2(8-h2+2h)=-2h2+4h+16.
∴帐篷的体积V(h)=(-2h2+4h+16)(1+$\frac{1}{3}$(h-1))=-$\frac{2}{3}{h}^{3}$+8h+$\frac{32}{3}$.
求导得V′(h)=-2h2+8.
令V′(h)=0得h=2或h=-2(舍).
当1<h<2时,V'(h)>0,V(h)为增函数;
当2<h<4时,V'(h)<0,V(h)为减函数.
所以当h=2时,V(h)最大.
答:当OO1为2m时,帐篷的体积最大.
点评 本小题主要考查利用导数研究函数的最大值和最小值的基础知识,以及运用数学知识解决实际问题的能力.


 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $({\frac{2}{3},±\frac{{2\sqrt{2}}}{3}})$ | B. | $({\frac{{2\sqrt{5}}}{3},±\frac{2}{3}})$ | C. | $({-\frac{2}{3},±\frac{{2\sqrt{2}}}{3}})$ | D. | $({-\frac{{2\sqrt{5}}}{3},±\frac{2}{3}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
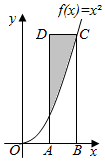 如图,点A的坐标为(1,0),点C的坐标为(2,4),函数f(x)=x2,四边形ABCD是矩形,则阴影区域的面积等于( )
如图,点A的坐标为(1,0),点C的坐标为(2,4),函数f(x)=x2,四边形ABCD是矩形,则阴影区域的面积等于( )| A. | $\frac{4}{3}$ | B. | $\frac{5}{3}$ | C. | 2 | D. | $\frac{7}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 1 | 2 | 3 | 4 | 5 |
| y | 7.0 | 6.5 | 5.5 | 3.8 | 2.2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
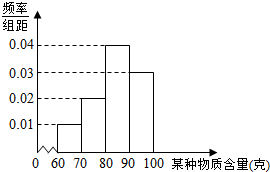 某企业对其生产的一批产品进行检测,得出每件产品中某种物质含量(单位:克)的频率分布直方图如图所示.
某企业对其生产的一批产品进行检测,得出每件产品中某种物质含量(单位:克)的频率分布直方图如图所示.| 产品级别 | C | B | A |
| 某种物质含量范围 | [60,70) | [70,80) | [80,90) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,三棱锥P-ABC中,△ABC是正三角形,PC⊥平面ABC,PC=AC=2,E为AC中点,EF⊥AP,垂足为F.
如图,三棱锥P-ABC中,△ABC是正三角形,PC⊥平面ABC,PC=AC=2,E为AC中点,EF⊥AP,垂足为F.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com