练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    5．对空间中有6个点两两连线，用红、黄两种颜色对这些染色，则同色三角形至少有5个．

    分析 根据5个点三边同色的三角形最少有0个，再加上第6个点A，则三边同色三角数至少为5个，然后证明少于5个是不可能的．

    解答 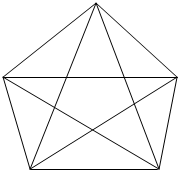解：如所给图，5个点三边同色的三角形最少有0个
    再加上第6个点A，则三边同色三角数至少为5个
    下证小于5个不行
    非同色三角形组成条件，就是只要有一个点出发的两条线段是非同色的，则其组成的三角一定为非同色的．所以，分以下情况：
    1，包含A点：其他五条为蓝色，组成5个非同色三角形
    2，未包含A点：因为5个点三边同色的三角形最少有0个，所以最多有10个非同色三角形
    如此，三边同色三角数至少为20-5-10=5个．
    故答案为：5．

    点评 本题主要考查了三角形的认识，正确理解三角形的定义，理解题目的含义是解决本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    15．现有两个“1”、两个“2”、一个“3”和一个“4”共六个数字，随意排列构成一个六位数，求相同的数字均不相邻的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．已知A={x|$\frac{6}{x+2}$＞1}，B={x|x-a＜0}．
    （1）若A∩B=（-2，0），求a的取值范围；
    （2）若A∩B=∅，求a的取值范围；
    （3）若A∩B=A，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．画出幂函数y=x，y=x2，y=x3，y=$\frac{1}{x}$，y=x${\;}^{\frac{1}{2}}$的图象．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．已知sin（x-$\frac{π}{4}$）=$\frac{\sqrt{2}}{10}$，x∈（π，$\frac{5π}{4}$），求cos（2x-$\frac{π}{4}$）的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．函数f（x）=cos（x+15°）+cos（x+75°）的值域为[-$\sqrt{3}$，$\sqrt{3}$]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．O为坐标原点，F为抛物线C：y2=4x的焦点，直线l：y=m（x-1）与抛物线C交于A，B两点，点A在第一象限，若S△AOF=3S△BOF，则实数m的值为$\sqrt{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．（x2-2）（1+$\frac{2}{x}$）5的展开式中x-1的系数为60．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    11．已知四棱锥的三视图（如图所示），则该四棱锥的体积为2，在该四棱锥的四个侧面中，面积最小的侧面面积是1．

    查看答案和解析>>

    同步练习册答案