
分析 (1)求出f(x)的导数,由导数的几何意义和切线方程,可得$f(\sqrt{e})=(2b-a)\sqrt{e}=\sqrt{e}$且$f'(\sqrt{e})=-2b-a=-3$,解方程可得a,b的值;
(2)求出f(x)的导数,以及f′(x)的最大值,由题意可得“当x∈[e,e2]时,有f(x)min≤f'(x)max+a”.对a分类讨论,①当$a≥\frac{1}{4}$时,②当$a<\frac{1}{4}$时,当-a≥0⇒a≤0时,当-a<0即$0<a<\frac{1}{4}$时,结合函数的单调性,求得f(x)的最小值,解不等式即可得到a的范围及a的最小值.
解答 解:(1)由已知得x>0,x≠1,
函数f(x)=$\frac{bx}{lnx}$-ax的导数为$f'(x)=\frac{b(lnx-1)}{{{{({lnx})}^2}}}-a$.
由切线方程为3x+y-4$\sqrt{e}$=0,可得:
$f(\sqrt{e})=(2b-a)\sqrt{e}=\sqrt{e}$且$f'(\sqrt{e})=-2b-a=-3$,解之得a=1,b=1;
(2)当b=1时,$f'(x)=\frac{lnx-1}{{{{({lnx})}^2}}}-a$=$-{({\frac{1}{lnx}})^2}+\frac{1}{lnx}-a=-{({\frac{1}{lnx}-\frac{1}{2}})^2}+\frac{1}{4}-a$,
所以当$\frac{1}{lnx}=\frac{1}{2}⇒x={e^2}$时,$f'{(x)_{max}}=\frac{1}{4}-a$.
而命题“若存在 ${x_1},{x_2}∈[{e,{e^2}}]$,使f(x1)≤f'(x2)+a成立”等价于
“当x∈[e,e2]时,有f(x)min≤f'(x)max+a”.
又当x∈[e,e2]时,$f'{(x)_{max}}=\frac{1}{4}-a$,所以$f'{(x)_{max}}+a=\frac{1}{4}$.
问题等价于:“当x∈[e,e2]时,有$f{(x)_{min}}≤\frac{1}{4}$”
①当$a≥\frac{1}{4}$时,f(x)在[e,e2]上为减函数,则$f{(x)_{min}}=f({e^2})=\frac{e^2}{2}-a{e^2}≤\frac{1}{4}$,
故$a≥\frac{1}{2}-\frac{1}{{4{e^2}}}$.
②当$a<\frac{1}{4}$时,由于$f'(x)=-{({\frac{1}{lnx}-\frac{1}{2}})^2}+\frac{1}{4}-a$在[e,e2]上的值域为$[{-a,\frac{1}{4}-a}]$.
当-a≥0⇒a≤0时,f'(x)≥0在[e,e2]恒成立,故f(x)在[e,e2]上为增函数,
于是$f{(x)_{min}}=f(e)=e-ae>\frac{1}{4}$,不合题意.
当-a<0即$0<a<\frac{1}{4}$时,由f'(x)的单调性和值域知,
存在唯一${x_0}∈({e,{e^2}})$使f'(x)=0,且满足:当x∈(e,x0)时,f'(x)<0,f(x)为减函数;
当$x∈({{x_0},{e^2}})$时,f'(x)>0,f(x)为增函数;所以$f{(x)_{min}}=f({x_0})=\frac{x_0}{{ln{x_0}}}-a{x_0}≤\frac{1}{4}$,${x_0}∈({e,{e^2}})$.所以$a≥\frac{1}{{ln{x_0}}}-\frac{1}{{4{x_0}}}>\frac{1}{{ln{e^2}}}-\frac{1}{4e}>\frac{1}{2}-\frac{1}{4}=\frac{1}{4}$,与$0<a<\frac{1}{4}$矛盾.
综上得a的最小值为$\frac{1}{2}-\frac{1}{{4{e^2}}}$.
点评 本题考查导数的运用:求切线的斜率和单调区间、极值和最值,考查不等式存在性问题的解法,运用分类讨论的思想方法是解题的关键,属于难题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
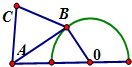 如图,半圆O的直径为1,A为直径延长线上的一点,OA=1,B为半圆上任意一点,以AB为一边作等边三角形ABC,则四边形OACB面积的最大值为$\frac{5\sqrt{3}}{16}$+$\frac{1}{2}$.
如图,半圆O的直径为1,A为直径延长线上的一点,OA=1,B为半圆上任意一点,以AB为一边作等边三角形ABC,则四边形OACB面积的最大值为$\frac{5\sqrt{3}}{16}$+$\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | 1 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,2,4,5} | B. | {2,4,5} | C. | {2,3,4} | D. | {3,4,5} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com