考点:二次函数的性质
专题:不等式的解法及应用
分析:原不等式等价为(ax-3)(x-2)<0,分a>0,a=0和a<0三种情况,分别解答,即可得到答案.
解答:
解:原不等式等价为(ax-3)(x-2)<0.
(1)当a=0时,原不等式为-3(x-2)<0,解得x>2.即原不等式的解集为(2,+∞).
(2)若a>0,则原不等式可化为a(x-
)(x-2)<0,即(x-
)(x-2)<0成立,
对应方程(x-
)(x-2)=0的根为x=2或x=
.
当
>2,即0<a<
时,不等式的解为(2,
).
当a=
时,不等式的解集为空集.
当
<2,即a>
时,不等式的解为(
,2).
(3)若a<0,则原不等式可化为a(x-
)(x-2)<0,
即(x-
)(x-2)>0成立,对应方程(x-
)(x-2)=0的根为x=2或x=
.
所以
<2,所以不等式的解集为(2,+∞)∪(-∞,
).
综上:(1)当a=0时,不等式的解集为(2,+∞).
(2)0<a<
时,不等式的解集为(2,
).
当a=
时,不等式的解集为空集.
当a>
时,不等式的解集为(
,2).
(3)当a<0时,不等式的解集为(2,+∞)∪(-∞,
).
点评:本题主要考查含有参数的不等式的解法,要对参数进行讨论,然后根据一元二次不等式的解法求不等式的解.



 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案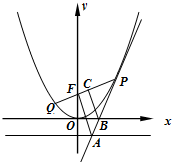 已知抛物线C:x2=4y的焦点为F,P是抛物线上异于原点的任意一点,直线PF与抛物线另一交点为点Q,设l是过点P的抛物线的切线,l与直线y=-1和x轴的交点分别为A,B.
已知抛物线C:x2=4y的焦点为F,P是抛物线上异于原点的任意一点,直线PF与抛物线另一交点为点Q,设l是过点P的抛物线的切线,l与直线y=-1和x轴的交点分别为A,B. 已知函数f(x)=x2-2ax+3在区间[-1,1]上有最小值,记作g(a).
已知函数f(x)=x2-2ax+3在区间[-1,1]上有最小值,记作g(a).