
设f(x)是定义在[-1,1]上的奇函数,且对任意的实数a,b∈[-1,1],当a+b
≠0时,都有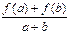 >0.
>0.
(1)若a>b,试比较f(a)与f(b)的大小;
(2)解不等式f(x -
-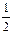 )<f(x-
)<f(x-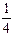 );
);
(3)如果g(x)=f(x-c)和h(x)=f(x-c2)这两个函数的定义域的交集是空集,求c的取值范围.
解:(1)任取x1,x2∈[-1,1]且设x1<x2,由奇函数的定义和题设不等式,得
f(x2)-f(x1)=f(x2)+f(-x1)=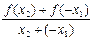 ·(x2-x1)>0,
·(x2-x1)>0,
∴f(x)在[-1,1]上是增函数.
∵a,b∈[-1,1]且a>b,∴f(a)>f(b) …………………………………4分
…………………………………4分
(2)∵f(x)是[-1,1]上的增函数
∴不等式f(x-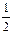 )<f(x-
)<f(x-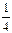 )等价于不等式组
)等价于不等式组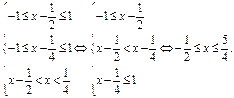
∴原不等式的解集为{x|-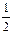 ≤x≤
≤x≤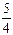 }.…………………………………8分
}.…………………………………8分
(3)设函数g(x)、h(x)的定义域分别是P和Q,则P={x|-1≤x-c≤1}={x|c-1≤x≤c+1},Q={x|-1≤x-c2≤1}={x|c2-1≤x≤c2+1},
若P∩Q=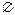 ,那么c+1<c2-1或c2+1<c-1.
,那么c+1<c2-1或c2+1<c-1.
解得c的取值范围是(-∞,-1)∪(2,+∞). ………………………………12分
解析


 阅读快车系列答案
阅读快车系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com