Question

16．在平面四边形ABCD中，点E、F分别是边AD、BC的中点，且AB=1，EF=$\sqrt{2}$，CD=$\sqrt{5}$，若$\overrightarrow{AD}•\overrightarrow{BC}$=15，则$\overrightarrow{AC}•\overrightarrow{BD}$的值为（　　）

• A． 13
• B． 14
• C． 15
• D． 16

Answer 1

分析 可作出图形，设AB∩DC=O，根据向量加法及数乘的几何意义便可得到$\overrightarrow{AB}=\overrightarrow{EF}+\frac{\overrightarrow{AD}-\overrightarrow{BC}}{2}$，$\overrightarrow{DC}=\overrightarrow{EF}+\frac{\overrightarrow{BC}-\overrightarrow{AD}}{2}$，从而得出$\overrightarrow{AB}+\overrightarrow{DC}=2\overrightarrow{EF}$，根据条件，两边平方即可求出$\overrightarrow{AB}•\overrightarrow{DC}=1$．而$\overrightarrow{AD}=\overrightarrow{OD}-\overrightarrow{OA}，\overrightarrow{BC}=\overrightarrow{OC}-\overrightarrow{OB}$，从而根据$\overrightarrow{AD}•\overrightarrow{BC}=15$便可以得到$\overrightarrow{OC}•\overrightarrow{OD}+\overrightarrow{OA}•\overrightarrow{OB}=15+\overrightarrow{OD}•\overrightarrow{OB}$$+\overrightarrow{OA}•\overrightarrow{OC}$，从而便可以求得$\overrightarrow{AC}•\overrightarrow{BD}=（15+\overrightarrow{OD}•\overrightarrow{OB}+\overrightarrow{OA}•\overrightarrow{OC}）$$-\overrightarrow{OC}•\overrightarrow{OB}-\overrightarrow{OA}•\overrightarrow{OD}$=$15-\overrightarrow{AB}•\overrightarrow{DC}$=14．

解答 解：如图所示，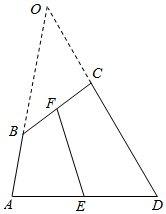

设AB∩DC=O，$\overrightarrow{AB}=\overrightarrow{AE}+\overrightarrow{EF}+\overrightarrow{FB}$=$\overrightarrow{EF}+\frac{\overrightarrow{AD}-\overrightarrow{BC}}{2}$，$\overrightarrow{DC}=\overrightarrow{DE}+\overrightarrow{EF}+\overrightarrow{FC}=\overrightarrow{EF}+\frac{\overrightarrow{BC}-\overrightarrow{AD}}{2}$；
∴$\overrightarrow{AB}+\overrightarrow{DC}=2\overrightarrow{EF}$；
∵$AB=1，EF=\sqrt{2}，CD=\sqrt{5}$，平方得，$1+5+2\overrightarrow{AB}•\overrightarrow{DC}=8$；
∴$\overrightarrow{AB}•\overrightarrow{DC}=1$；
又$\overrightarrow{AD}•\overrightarrow{BC}=15$；
即$（\overrightarrow{OD}-\overrightarrow{OA}）•（\overrightarrow{OC}-\overrightarrow{OB}）$=$\overrightarrow{OD}•\overrightarrow{OC}-\overrightarrow{OD}•\overrightarrow{OB}-\overrightarrow{OA}•\overrightarrow{OC}+\overrightarrow{OA}•\overrightarrow{OB}=15$；
∴$\overrightarrow{OC}•\overrightarrow{OD}+\overrightarrow{OA}•\overrightarrow{OB}$=$15+\overrightarrow{OD}•\overrightarrow{OB}+\overrightarrow{OA}•\overrightarrow{OC}$；
∴$\overrightarrow{AC}•\overrightarrow{BD}=（\overrightarrow{OC}-\overrightarrow{OA}）•（\overrightarrow{OD}-\overrightarrow{OB}）$
=$\overrightarrow{OC}•\overrightarrow{OD}-\overrightarrow{OC}•\overrightarrow{OB}-\overrightarrow{OA}•\overrightarrow{OD}$$+\overrightarrow{OA}•\overrightarrow{OB}$
=$（15+\overrightarrow{OD}•\overrightarrow{OB}+\overrightarrow{OA}•\overrightarrow{OC}）$$-\overrightarrow{OC}•\overrightarrow{OB}-\overrightarrow{OA}•\overrightarrow{OD}$
=$15+（\overrightarrow{OD}-\overrightarrow{OC}）•\overrightarrow{OB}$$+\overrightarrow{OA}•（\overrightarrow{OC}-\overrightarrow{OD}）$
=$15-\overrightarrow{DC}•\overrightarrow{OB}+\overrightarrow{OA}•\overrightarrow{DC}$
=$15+（\overrightarrow{OA}-\overrightarrow{OB}）•\overrightarrow{DC}$
=$15-\overrightarrow{AB}•\overrightarrow{DC}$
=15-1
=14．
故选B．

点评 考查向量加法、减法和数乘的几何意义，以及向量的数乘运算，向量数量积的运算．