
已知二次函数f(x)=ax2+bx+c(a>0).
(Ⅰ)(i)若b=﹣2,且f(x)在(1,+∞)上为单调递增函数,求实数a的取值范围;
(ii)若b=﹣1,c=1,当x∈[0,1]时,|f(x)|的最大值为1,求实数a的取值范围;
(Ⅱ)若f(0)≥1,f(1)≥1,f(x)=0的有两个小于1的不等正根,求a的最小正整数值.
(Ⅰ)(i)[1,+∞);(ii)(0,1];(Ⅱ)5
【解析】
试题分析:(Ⅰ)(i)若b=﹣2,则f(x)=ax2﹣2x+c(a>0)的图象是开口朝上且以直线x= 为对称轴的抛物线.若f(x)在(1,+∞)上为单调递增函数,则
为对称轴的抛物线.若f(x)在(1,+∞)上为单调递增函数,则 ≤1,解得a≥1,即实数a的取值范围为[1,+∞);(ii)若b=﹣1,c=1,则f(x)=ax2﹣x+1(a>0)的图象是开口朝上且以直线x=
≤1,解得a≥1,即实数a的取值范围为[1,+∞);(ii)若b=﹣1,c=1,则f(x)=ax2﹣x+1(a>0)的图象是开口朝上且以直线x=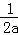 为对称轴的抛物线,若当x∈[0,1]时,|f(x)|的最大值为1,则
为对称轴的抛物线,若当x∈[0,1]时,|f(x)|的最大值为1,则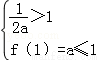 或
或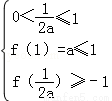 解得0<a<
解得0<a<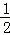 ,或
,或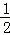 ≤a≤1,所以实数a的取值范围为(0,1];(Ⅱ)若f(0)≥1,f(1)≥1,f(x)=0的有两个小于1的不等正根,则
≤a≤1,所以实数a的取值范围为(0,1];(Ⅱ)若f(0)≥1,f(1)≥1,f(x)=0的有两个小于1的不等正根,则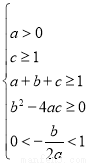
解得a>4,故a的最小正整数值为5.
试题解析:(Ⅰ)(i)若b=﹣2,
则f(x)=ax2﹣2x+c(a>0)的图象是开口朝上且以直线x= 为对称轴的抛物线.
为对称轴的抛物线.
若f(x)在(1,+∞)上为单调递增函数,则 ≤1,解得a≥1,
≤1,解得a≥1,
即实数a的取值范围为[1,+∞)
(ii)若b=﹣1,c=1,
则f(x)=ax2﹣x+1(a>0)的图象是开口朝上且以直线x=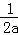 为对称轴的抛物线.
为对称轴的抛物线.
若当x∈[0,1]时,|f(x)|的最大值为1,
则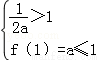 或
或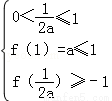 ,
,
解得0<a<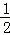 ,或
,或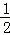 ≤a≤1
≤a≤1
综上所述:0<a≤1
即实数a的取值范围为(0,1]
(Ⅱ)若f(0)≥1,f(1)≥1,f(x)=0的有两个小于1的不等正根,
则
由b2>4ac>4a(1﹣a﹣b)得:
b2+4ab+4a2=(b+2a)2>4a,
即b+2a>2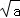 ,
,
即b>2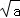 ﹣2a,…①
﹣2a,…①
由b2>4ac≥4a得:
b<﹣2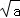 …②
…②
由①②得:
2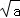 ﹣2a<﹣2
﹣2a<﹣2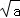 ,
,
解得a>4,
故a的最小正整数值为5.
考点:1.二次函数的图象与性质;2.不等式的性质


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:高中数学 来源:2015届湖北省高二5月月考理科数学试卷(解析版) 题型:选择题
下面使用的类比推理中恰当的是( )
A.“若 ,则
,则 ”类比得出“若
”类比得出“若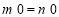 ,则
,则 ”
”
B.“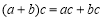 ”类比得出“
”类比得出“ ”
”
C.“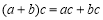 ”类比得出“
”类比得出“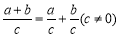 ”
”
D.“ ”类比得出“
”类比得出“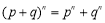 ”
”
查看答案和解析>>
科目:高中数学 来源:2015届湖北省高二5月月考文科数学试卷(解析版) 题型:选择题
给出如下四个命题:
①若“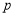 且
且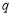 ”为假命题,则
”为假命题,则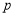 、
、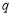 均为假命题;
均为假命题;
②命题“若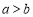 ,则
,则 ”的否命题为“若
”的否命题为“若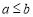 ,则
,则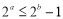 ”;
”;
③“ ”的否定是“
”的否定是“ ”;
”;
④在△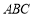 中,“
中,“ ”是“
”是“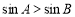 ”的充要条件.
”的充要条件.
其中不正确的命题的个数是( )
A.4 B.3 C.2 D.1
查看答案和解析>>
科目:高中数学 来源:2015届浙江省金华十校高二下学期期末考试理科数学试卷(解析版) 题型:填空题
已知函数f(x)=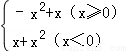 ,对任意的x∈[0,1]恒有f(x+a)≤f(x)成立,则实数a的取值范围是 .
,对任意的x∈[0,1]恒有f(x+a)≤f(x)成立,则实数a的取值范围是 .
查看答案和解析>>
科目:高中数学 来源:2015届浙江省金华十校高二下学期期末考试理科数学试卷(解析版) 题型:选择题
已知△ABC的顶点A(3,0),B(0,1),C(1,1),P(x,y)在△ABC内部(包括边界),若目标函数z= (a≠0)取得最大值时的最优解有无穷多组,则点(a,b)的轨迹可能是( )
(a≠0)取得最大值时的最优解有无穷多组,则点(a,b)的轨迹可能是( )

查看答案和解析>>
科目:高中数学 来源:2015届浙江省金华十校高二下学期期末考试文科数学试卷(解析版) 题型:填空题
设某几何体的三视图如图(尺寸的长度单位为m)则该几何体的体积为 _________ m3.

查看答案和解析>>
科目:高中数学 来源:2015届浙江省绍兴市高二下学期期末考试文科数学试卷(解析版) 题型:填空题
设M是△ABC内一点, ·
·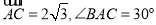 ,定义
,定义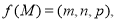 其中
其中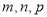 分别是△MBC,△MAC,△MAB的面积,若
分别是△MBC,△MAC,△MAB的面积,若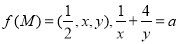 ,则
,则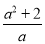 的取值范围是 .
的取值范围是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com