
如果函数f(x)在区间D上是凸函数,那么对于区间D内的任意x1,x2,…,xn,都有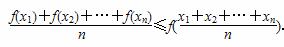 .若y=sinx在区间(0,π)上是凸函数,那么在△ABC中,sinA+sinB+sinC的最大值是________.
.若y=sinx在区间(0,π)上是凸函数,那么在△ABC中,sinA+sinB+sinC的最大值是________.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
设z1、z2是复数,则下列命题中的假命题是( )
A.若|z1-z2|=0,则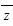 1=
1=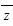 2
2
B.若z1=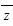 2,则
2,则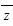 1=z2
1=z2
C.若|z1|=|z2|,则z1·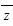 1=z2·
1=z2·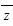 2
2
D.若|z1|=|z2|,则z =z
=z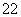
查看答案和解析>>
科目:高中数学 来源: 题型:
类比“两角和与差的正弦公式”的形式,对于给定的两个函数:S(x)=ax-a-x,C(x)=ax+a-x,其中a>0,且a≠1,下面正确的运算公式是( )
①S(x+y)=S(x)C(y)+C(x)S(y);
②S(x-y)=S(x)C(y)-C(x)S(y);
③2S(x+y)=S(x)C(y)+C(x)S(y);
④2S(x-y)=S(x)C(y)-C(x)S(y).
A.①② B.③④
C.①④ D.②③
查看答案和解析>>
科目:高中数学 来源: 题型:
椭圆与双曲线有许多优美的对偶性质,如对于椭圆有如下命题:AB是椭圆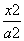 +
+ =1(a>b>0)的不平行于对称轴且不过原点的弦,M为AB的中点,则kOM·kAB=-
=1(a>b>0)的不平行于对称轴且不过原点的弦,M为AB的中点,则kOM·kAB=-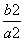 .那么对于双曲线则有如下命题:AB是双曲线
.那么对于双曲线则有如下命题:AB是双曲线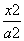 -
- =1(a>0,b>0)的不平行于对称轴且不过原点的弦,M为AB的中点,则kOM·kAB=________.
=1(a>0,b>0)的不平行于对称轴且不过原点的弦,M为AB的中点,则kOM·kAB=________.
查看答案和解析>>
科目:高中数学 来源: 题型:
以下是对命题“若两个正实数a1,a2满足a +a
+a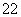 =1,则a1+a2≤
=1,则a1+a2≤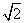 ”的证明过程:证明:构造函数f(x)=(x-a1)2+(x-a2)2=2x2-2(a1+a2)x+1,因为对一切实数x,恒有f(x)≥0,所以Δ≤0,从而得4(a1+a2)2-8≤0,所以a1+a2≤
”的证明过程:证明:构造函数f(x)=(x-a1)2+(x-a2)2=2x2-2(a1+a2)x+1,因为对一切实数x,恒有f(x)≥0,所以Δ≤0,从而得4(a1+a2)2-8≤0,所以a1+a2≤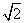 .
.
根据上述证明方法,若n个正实数a1、a2、…、an满足a +a
+a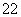 +…+a
+…+a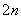 =1时,你能得到的结论为____________________(不必证明).
=1时,你能得到的结论为____________________(不必证明).
查看答案和解析>>
科目:高中数学 来源: 题型:
用数学归纳法证明:(n+1)+(n+2)+…+(n+n)= (n∈N*)的第二步中,当n=k+1时等式左边与n=k时等式左边的差等于________.
(n∈N*)的第二步中,当n=k+1时等式左边与n=k时等式左边的差等于________.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,在△ABC和△ACD中,∠ACB=∠ADC=90°,∠BAC=∠CAD,⊙O是以AB为直径的圆,DC的延长线与AB的延长线交于点E.
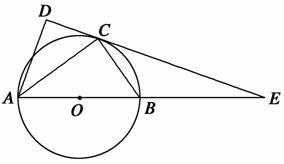
(1)求证:DC是⊙O的切线;
(2)若EB=6,EC=6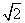 ,求BC的长.
,求BC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com