练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图，在△ABC和△ACD中，∠ACB＝∠ADC＝90°，∠BAC＝∠CAD，⊙O是以AB为直径的圆，DC的延长线与AB的延长线交于点E.

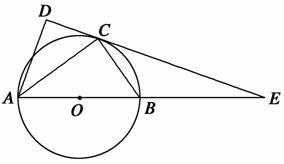
    (1)求证：DC是⊙O的切线；

    (2)若EB＝6，EC＝6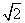，求BC的长．


     (1)∵AB是⊙O的直径，∠ACB＝90°，

    ∴点C在⊙O上，

    连接OC，可得∠OCA＝∠OAC＝∠DAC，∴OC∥AD，

    又∵AD⊥DC，∴DC⊥OC，

    ∵OC为半径，

    ∴DC是⊙O的切线．

    (2)∵DC是⊙O的切线，

    ∴EC2＝EB·EA.

    又∵EB＝6，EC＝6，

    ∴EA＝12，AB＝6.

    ∵∠ECB＝∠EAC，∠CEB＝∠AEC，

    ∴△ECB△EAC，

    ∴＝＝，∴AC＝BC.

    ∵AC2＋BC2＝AB2＝36，∴BC＝2.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    如果函数f(x)在区间D上是凸函数，那么对于区间D内的任意x1，x2，…，xn，都有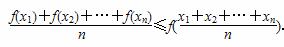．若y＝sinx在区间(0，π)上是凸函数，那么在△ABC中，sinA＋sinB＋sinC的最大值是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知正项数列{an}中，对于一切的n∈N*均有a≤an－an＋1成立．

    (1)证明：数列{an}中的任意一项都小于1；

    (2)探究an与的大小，并证明你的结论．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，圆O上一点C在直径AB上的射影为D，点D在半径OC上的射影为E，若AB＝3AD，则的值为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如下图，点D在⊙O的弦AB上移动，AB＝4，连接OD，过点D作OD的垂线交⊙O于点C，则CD的最大值为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，△ABO三边上的点C、D、E都在⊙O上，已知AB∥DE，AC＝CB.

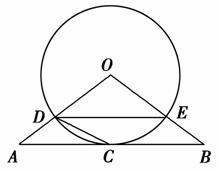
    (1)求证：直线AB是⊙O的切线；

    (2)若AD＝2，且tan∠ACD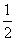＝，求⊙O的半径r的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若直线的参数方程为(t为参数)，则直线的倾斜角为(　　)

    A．30°                                                          B．60°

    C．120°                                                        D．150°

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    以直角坐标系的原点O为极点，x轴的正半轴为极轴，且两个坐标坐标系取相等的单位长度．已知直线l经过点P(1,1)，倾斜角α＝.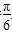

    (1)写出直线l的参数方程；

    (2)设l与圆ρ＝2相交于两点A、B，求点P到A、B两点的距离之积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    用反证法证明：若整系数一元二次方程ax2＋bx＋c＝0(a≠0)有有理数根，那么a、b、c中至少有一个是偶数．用反证法证明时，下列假设正确的是(　　)

    A．假设a，b，c都是偶数

    B．假设a，b，c都不是偶数

    C．假设a，b，c至多有一个偶数

    D．假设a，b，c至多有两个偶数

    查看答案和解析>>

    同步练习册答案