练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    椭圆与双曲线有许多优美的对偶性质，如对于椭圆有如下命题：AB是椭圆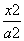＋＝1(a>b>0)的不平行于对称轴且不过原点的弦，M为AB的中点，则kOM·kAB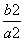＝－.那么对于双曲线则有如下命题：AB是双曲线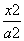－＝1(a>0，b>0)的不平行于对称轴且不过原点的弦，M为AB的中点，则kOM·kAB＝________.


    　


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    小波以游戏方式决定是参加学校合唱团还是参加学校排球队．游戏规则为：以O为起点，再从A1，A2，A3，A4，A5，A6，A7，A8(如图)这8个点中任取两点分别为终点得到两个向量，记这两个向量的数量积为X.若X＝0就参加学校合唱团，否则就参加学校排球队．

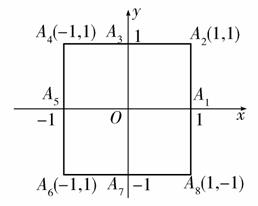
    (1)求小波参加学校合唱团的概率；

    (2)求X的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知复数(1－2i)i(其中i为虚数单位)在复平面内对应的点M在直线y＝mx＋n上，其中mn>0，求＋的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    将正整数排成下表：

    则在表中数字2014出现在(　　)

    A．第44行第78列                                       B．第45行第78列

    C．第44行第77列                                       D．第45行第77列

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如果函数f(x)在区间D上是凸函数，那么对于区间D内的任意x1，x2，…，xn，都有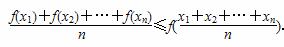．若y＝sinx在区间(0，π)上是凸函数，那么在△ABC中，sinA＋sinB＋sinC的最大值是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知 (a、t均为正实数)，则类比以上等式，可推测a、t的值，a＋t＝(　　)

    A．48                                                           B．55 

    C．41                                                           D．30

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知命题：若数列{an}为等差数列，且am＝a，an＝b(m≠n，m、n∈N*)，则am＋n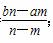＝；现已知等比数列{bn}(n∈N*)，bm＝a，bn＝b(m≠n，m、n∈N*)，类比上述结论，得出在等比数列{bn}中，bn＋m＝________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知f(n)＝1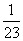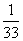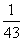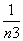＋＋＋＋…＋，g(n)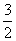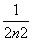＝－，n∈N*.

    (1)当n＝1,2,3时，试比较f(n)与g(n)的大小；

    (2)猜想f(n)与g(n)的大小关系，并给出证明．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，△ABO三边上的点C、D、E都在⊙O上，已知AB∥DE，AC＝CB.

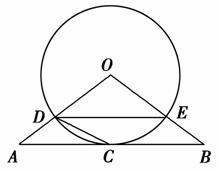
    (1)求证：直线AB是⊙O的切线；

    (2)若AD＝2，且tan∠ACD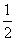＝，求⊙O的半径r的长．

    查看答案和解析>>

    同步练习册答案