
| 4+4 |
| 2+2 |


科目:高中数学 来源: 题型:
| 3 |
| α |
| 2 |
| π |
| 6 |
| 6 |
| 5 |
| π |
| 2 |
| π |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
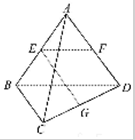 如图:已知空间四边形ABCD的边长和对角线的长都为2,点E,F,G分别是AB,AD,DC的中点求下列数量积:
如图:已知空间四边形ABCD的边长和对角线的长都为2,点E,F,G分别是AB,AD,DC的中点求下列数量积:| AB |
| AC |
| AD |
| BD |
| GF |
| AC |
| EF |
| BC |
查看答案和解析>>
科目:高中数学 来源: 题型:
| OP |
| e1 |
| e2 |
| e1 |
| e2 |
|
| ||
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
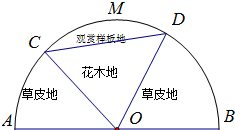 某园林公司计划在一块O为圆心,R(R为常数)为半径的半圆形(如图)地上种植花草树木,其中弓形CMDC区域用于观赏样板地,△OCD区域用于种植花木出售,其余区域用于种植草皮出售.已知观赏样板地的成本是每平方米2元,花木的利润是每平方米8元,草皮的利润是每平方米3元.
某园林公司计划在一块O为圆心,R(R为常数)为半径的半圆形(如图)地上种植花草树木,其中弓形CMDC区域用于观赏样板地,△OCD区域用于种植花木出售,其余区域用于种植草皮出售.已知观赏样板地的成本是每平方米2元,花木的利润是每平方米8元,草皮的利润是每平方米3元. |
| CMD |
| 1 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com