
已知函数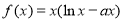 有两个极值点,则实数
有两个极值点,则实数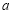 的取值范围是 .
的取值范围是 .
科目:高中数学 来源:2015届福建省高二下学期期末考试理科数学试卷(解析版) 题型:解答题
如图所示,将一矩形花坛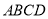 扩建成一个更大的矩形花坛
扩建成一个更大的矩形花坛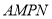 ,要求
,要求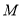 在
在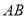 的延长线上,
的延长线上,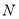 在
在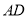 的延长线上,且对角线
的延长线上,且对角线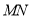 过
过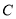 点.已知
点.已知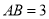 米,
米,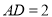 米。
米。

(1)设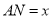 (单位:米),要使花坛
(单位:米),要使花坛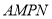 的面积大于32平方米,求
的面积大于32平方米,求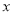 的取值范围;
的取值范围;
(2)若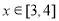 (单位:米),则当
(单位:米),则当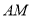 ,
,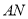 的长度分别是多少时,花坛
的长度分别是多少时,花坛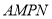 的面积最大?并求出最大面积.
的面积最大?并求出最大面积.
查看答案和解析>>
科目:高中数学 来源:2015届福建省高二下学期期末考理科数学试卷(解析版) 题型:解答题
已知函数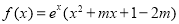 ,其中
,其中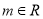 .
.
(Ⅰ)当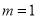 时,求函数
时,求函数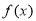 的单调递增区间;
的单调递增区间;
(Ⅱ)证明:对任意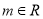 ,函数
,函数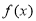 的图象在点
的图象在点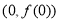 处的切线恒过定点;
处的切线恒过定点;
(Ⅲ)是否存在实数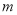 的值,使得函数
的值,使得函数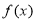 在
在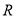 上存在最大值或最小值?若存在,求出实数
上存在最大值或最小值?若存在,求出实数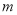 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2015届福建省高二下学期期末考理科数学试卷(解析版) 题型:选择题
某车间加工零件的数量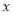 与加工时间
与加工时间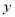 的统计数据如下表:
的统计数据如下表:
零件数 | 10 | 20 | 30 |
加工时间 | 21 | 30 | 39 |
现已求得上表数据的回归方程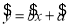 中的
中的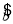 值为0.9,则据此回归模型可以预测,加工100个零件所需要的加工时间约为
值为0.9,则据此回归模型可以预测,加工100个零件所需要的加工时间约为
A.84分钟 B.94分钟 C.102分钟 D.112分钟
查看答案和解析>>
科目:高中数学 来源:2015届福建省高二下学期期中考理科数学试卷(解析版) 题型:解答题
已知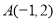 为曲线
为曲线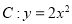 上的点,直线
上的点,直线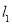 过点
过点 ,且与曲线
,且与曲线 相切,直线
相切,直线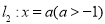 交曲线
交曲线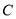 于
于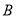 ,交直线
,交直线 于点
于点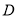 .
.

(1) 求直线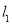 的方程;
的方程;
(2)设 的面积为
的面积为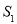 ,求
,求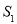 的值;
的值;
(3)设由曲线 ,直线
,直线 ,
,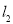 所围成的图形的面积为
所围成的图形的面积为 ,求证
,求证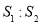 的值为与
的值为与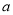 无关的常数.
无关的常数.
查看答案和解析>>
科目:高中数学 来源:2015届福建省高二上学期期末考理科数学试卷(解析版) 题型:选择题
若直线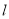 过点
过点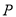 (1,0)与双曲线
(1,0)与双曲线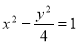 只有一个公共点,则这样的直线有
只有一个公共点,则这样的直线有
A.4条 B.3条 C. 2条 D.1条
查看答案和解析>>
科目:高中数学 来源:2015届福建省晋江市高二下学期期末理科数学试卷(解析版) 题型:填空题
已知随机变量X服从正态分布N( 0,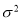 ),且P(-2≤X≤0)=0.4,则P(X>2)=________.
),且P(-2≤X≤0)=0.4,则P(X>2)=________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com