
【题目】已知数列{an},{bn}均为各项都不相等的数列,Sn为{an}的前n项和,an+1bn=Sn+1(n∈N).
(1)若a1=1,bn= ![]() ,求a4的值;
,求a4的值;
(2)若{an}是公比为q的等比数列,求证:存在实数λ,使得{bn+λ}为等比数列;
(3)若{an}的各项都不为零,{bn}是公差为d的等差数列,求证:a2 , a3 , …,an…成等差数列的充要条件是d= ![]() .
.
【答案】
(1)解:∵an+1bn=Sn+1,a1=1,bn= ![]() ,
,
∴a2= ![]() =
= ![]() =4,
=4,
a3= ![]() =
= ![]() =6,
=6,
a4= ![]() =
= ![]() =8
=8
(2)证明:设an=a1qn﹣1(q≠1),则Sn= ![]() ,
,
∵an+1bn=Sn+1,
∴bn= ![]() =
= ![]() ,
,
∵ ![]() =
= 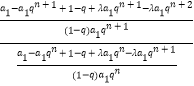 =
= ![]() 为常数,
为常数,
∴﹣1+λ﹣λq=0,即λ= ![]() ,
,
故存在实数λ= ![]() ,使得{bn+λ}为等比数列
,使得{bn+λ}为等比数列
(3)证明:∵数列{bn}是公差为d的等差数列,
∴当n≥2时,an+1bn﹣an(bn﹣d)=an,
即(an+1﹣an)bn=(1﹣d)an,
∵数列{an}的各项都不为零,
∴an+1﹣an≠0,1﹣d≠0,
∴当n≥2时, ![]() =
= ![]() ,
,
当n≥3时, ![]() =
= ![]() ,
,
两式相减得:当n≥3时, ![]() ﹣
﹣ ![]() =
= ![]() =
= ![]() .
.
先证充分性:
由d= ![]() 可知
可知 ![]() ﹣
﹣ ![]() =1,
=1,
∴当n≥3时, ![]() +1=
+1= ![]() ,
,
又∵an≠0,
∴an+1﹣an=an﹣an﹣1,
即a2,a3,…,an…成等差数列;
再证必要性:
∵a2,a3,…,an…成等差数列,
∴当n≥3时,an+1﹣an=an﹣an﹣1,
∴ ![]() ﹣
﹣ ![]() =
= ![]() ﹣
﹣ ![]() =1=
=1= ![]() ,
,
∴d= ![]() .
.
综上所述,a2,a3,…,an…成等差数列的充要条件是d= ![]()
【解析】(1)直接代入计算即可;(2)通过设an=a1qn﹣1(q≠1),利用等比数列的求和公式及an+1bn=Sn+1,计算可知bn= ![]() ,进而化简即得结论;(3)通过数列{bn}是公差为d的等差数列,对an+1bn﹣an(bn﹣d)=an变形可知
,进而化简即得结论;(3)通过数列{bn}是公差为d的等差数列,对an+1bn﹣an(bn﹣d)=an变形可知 ![]() =
= ![]() (n≥2)、
(n≥2)、 ![]() =
= ![]() (n≥3),从而
(n≥3),从而 ![]() ﹣
﹣ ![]() =
= ![]() (n≥3),然后分别证明充分性、必要性即可.
(n≥3),然后分别证明充分性、必要性即可.
【考点精析】本题主要考查了等比数列的通项公式(及其变式)和数列的通项公式的相关知识点,需要掌握通项公式:![]() ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能正确解答此题.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能正确解答此题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是正方形.点E是棱PC的中点,平面ABE与棱PD交于点F.
(Ⅰ)求证:AB∥EF;
(Ⅱ)若PA=AD,且平面PAD⊥平面ABCD,求证:AF⊥平面PCD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,圆C1:(x﹣1)2+y2=2,圆C2:(x﹣m)2+(y+m)2=m2 . 圆C2上存在点P满足:过点P向圆C1作两条切线PA,PB,切点为A,B,△ABP的面积为1,则正数m的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 如图,在四棱锥P﹣ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD= ![]() ,PA⊥PD,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AB=BC=1,O为AD中点.
,PA⊥PD,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AB=BC=1,O为AD中点.

(1) 求直线PB与平面POC所成角的余弦值;
(2)线段![]() 上是否存在一点
上是否存在一点![]() ,使得二面角
,使得二面角![]() 的余弦值为
的余弦值为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了普及环保知识,增强环保意识,某大学从理工类专业的A班和文史类专业的B班各抽取20名同学参加环保知识测试.统计得到成绩与专业的列联表如下所示:
优秀 | 非优秀 | 总计 | |
A班 | 14 | 6 | 20 |
B班 | 7 | 13 | 20 |
总计 | 21 | 19 | 40 |
则下列说法正确的是 ( )
A. 有99%的把握认为环保知识测试成绩与专业有关
B. 有99%的把握认为环保知识测试成绩与专业无关
C. 有95%的把握认为环保知识测试成绩与专业有关
D. 有95%的把握认为环保知识测试成绩与专业无关
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】PM2.5(单位:μg/m3)表示每立方米空气中可入肺颗粒物的含量,这个值越高,空气污染越严重.PM2.5的浓度与空气质量类别的关系如下表所示:

从甲城市2016年9月份的30天中随机抽取15天,这15天的PM2.5的日均浓度指数数据如茎叶图所示.
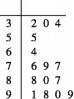
(1)试估计甲城市在2016年9月份的30天中,空气质量类别为优或良的天数;
(2)从甲城市的这15个监测数据中任取2个,设X是空气质量类别为优或良的天数,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知抛物线y2=2px(p>0)上一点P( ![]() ,m)到准线的距离与到原点O的距离相等,抛物线的焦点为F.
,m)到准线的距离与到原点O的距离相等,抛物线的焦点为F.
(1)求抛物线的方程;
(2)若A为抛物线上一点(异于原点O),点A处的切线交x轴于点B,过A作准线的垂线,垂足为点E.试判断四边形AEBF的形状,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,已知圆![]() 的圆心坐标为
的圆心坐标为![]() ,半径为
,半径为![]() ,以坐标原点为极点,
,以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,直线l的参数方程为:
轴的正半轴为极轴建立极坐标系,直线l的参数方程为:![]() (
(![]() 为参数).
为参数).
(1)求圆![]() 和直线l的极坐标方程;
和直线l的极坐标方程;
(2)点![]() 的极坐标为
的极坐标为![]() ,直线l与圆
,直线l与圆![]() 相交于A,B,求
相交于A,B,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com