
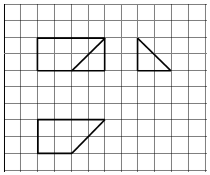
 如图:网格纸上的小正方形边长都为1,粗线画出的是某几何体的三视图,则该几何体的体积为( )
如图:网格纸上的小正方形边长都为1,粗线画出的是某几何体的三视图,则该几何体的体积为( )| A. | 4 | B. | $\frac{16}{3}$ | C. | $\frac{20}{3}$ | D. | 8 |
分析 由三视图知该几何体是一个直三棱柱切去一个三棱锥所得的组合体,由三视图求出几何元素的长度、判断出线面的位置关系,由柱体、锥体的体积公式求出几何体的体积.
解答 解:由三视图知该几何体是一个直三棱柱切去一个三棱锥所得的组合体,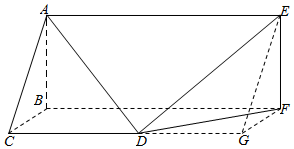
其直观图如图所示:
底面是等腰三角形,AB=BC=2棱长是4,
其中D是CG的中点,
∵BF⊥平面EFG,∴BF⊥EF,
∵EF⊥FG,BF∩FG=F,
∴EF⊥平面BFGC,
∴组合体的体积:
V=V三棱柱ABC-EFG-V三棱锥E-DFG
═$\frac{1}{2}×2×2×4-\frac{1}{3}×\frac{1}{2}×2×2×2$=$\frac{20}{3}$,
故选:C.
点评 本题考查三视图求几何体的体积,由三视图正确复原几何体是解题的关键,考查空间想象能力.


科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,底面ABCD是正方形,平面PCD⊥底面ABCD,PD⊥CD,PD=CD,E为PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,平面PCD⊥底面ABCD,PD⊥CD,PD=CD,E为PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 16π | B. | 32π | C. | 8π | D. | 64π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
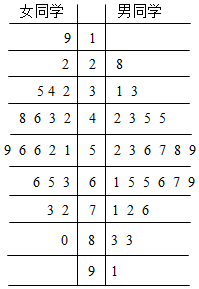 某课题组对全班45名同学的饮食习惯进行了一次调查,并用茎叶图表示45名同学的饮食指数.说明:如图中饮食指数低于70的人被认为喜食蔬菜,饮食指数不低于70的人被认为喜食肉类
某课题组对全班45名同学的饮食习惯进行了一次调查,并用茎叶图表示45名同学的饮食指数.说明:如图中饮食指数低于70的人被认为喜食蔬菜,饮食指数不低于70的人被认为喜食肉类| 喜食蔬菜 | 喜食肉类 | 合计 | |
| 男同学 | |||
| 女同学 | |||
| 合计 |
| P(K2≥k) | 0.100 | 0.05 | 0.010 |
| k | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
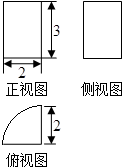
| A. | 3π+12 | B. | 5π | C. | 5π+12 | D. | 8π+12 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 某组合体的三视图如图示,则该组合体的表面积为( )
某组合体的三视图如图示,则该组合体的表面积为( )| A. | $(6+2\sqrt{2})π+12$ | B. | 8(π+1) | C. | 4(2π+1) | D. | $(12+2\sqrt{2})π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
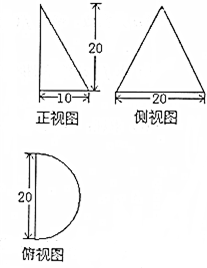 已知某几何体的三视图如图所示,根据图中标出的尺寸(单位:cm),可得这个几何体的侧面积为( )
已知某几何体的三视图如图所示,根据图中标出的尺寸(单位:cm),可得这个几何体的侧面积为( )| A. | (200+100$\sqrt{3}$)cm2 | B. | (200+100π)cm2 | C. | (200+50$\sqrt{5}$π)cm2 | D. | (300+50π)cm2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
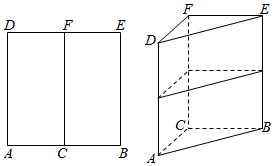
 几何体EFG-ABCD的面ABCD,ADGE,DCFG均为矩形,AD=DC=1,AE=$\sqrt{2}$.
几何体EFG-ABCD的面ABCD,ADGE,DCFG均为矩形,AD=DC=1,AE=$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
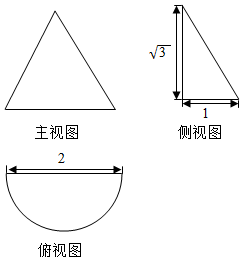 某几何体的三视图如图所示,则此几何体的体积为( )
某几何体的三视图如图所示,则此几何体的体积为( )| A. | $\frac{\sqrt{3}}{6}$π | B. | $\frac{\sqrt{3}}{3}$π | C. | $\sqrt{3}$π | D. | π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com