
分析 (1)写出直线的斜率利用判别式求最值;
(2)M,N把圆弧分割成1:3的两部分,则CM⊥CN,确定圆心C到直线l的距离d=$\frac{2}{\sqrt{1+{k}^{2}}}$=$\sqrt{2}$,即可得出结论.
解答 解:(1)直线l的方程可化为y=$\frac{m}{{m}^{2}+1}$x-$\frac{4m}{{m}^{2}+1}$,斜率k=$\frac{m}{{m}^{2}+1}$,
即km2-m+k=0,k=0时,m=0成立;
又∵△≥0,∴1-4k2≥0,
所以,斜率k的取值范围是[-$\frac{1}{2}$,$\frac{1}{2}$].
(2)M,N把圆弧分割成1:3的两部分,则CM⊥CN.由(1)知l的方程为y=k(x-4),其中|k|≤$\frac{1}{2}$;
圆C的圆心为C(4,-2),半径r=2;圆心C到直线l的距离d=$\frac{2}{\sqrt{1+{k}^{2}}}$=$\sqrt{2}$
∴k=±1
∴直线l的方程y=±(x-4).
点评 本题考查直线与圆及不等式知识的综合应用,考查点到直线的距离公式,考查学生分析解决问题的能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
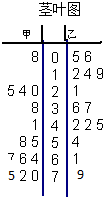 为了调查甲、乙两个网站受欢迎的程度,随机选取了14天,统计上午8:00~10:00间各自的点击量,得如图所示的统计图,根据统计图:
为了调查甲、乙两个网站受欢迎的程度,随机选取了14天,统计上午8:00~10:00间各自的点击量,得如图所示的统计图,根据统计图:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{2}}}{3}$ | B. | $2\sqrt{3}$ | C. | $\sqrt{3}$ | D. | $\frac{{\sqrt{2}}}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | -1 | D. | 不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x≥-2} | B. | {x|x>-1} | C. | {x|x<-1} | D. | {x|x≤-2} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com