练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    直线l：x=1与圆x2+y2-2y=0的位置关系是
     
    ．
    考点：直线与圆的位置关系
    专题：直线与圆
    分析：把圆的方程化为标准形式，根据圆心和半径可得它和直线l：x=1的关系．
    解答： 解：圆x2+y2-2y=0，即 x2+（y-1）2 =1，表示以（0，1）为圆心、半径等于1的圆，
    故此圆和直线l：x=1相切，
    故答案为：相切．
    点评：本题主要考查直线和圆的位置关系判定，圆的标准方程，属于基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知抛物线C1：x2=4py，圆C2：x2+（y-p）2=p2，直线l：y=
    1
    2
    x+p，其中p＞0，直线l与C1，C2的四个交点按横坐标从小到大依次为A，B，C，D，则
    AB
    •
    CD
    的值为（　　）
    A、
    p2
    4
    B、
    p2
    3
    C、
    p2
    2
    D、p2

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若直线a∥b，且a⊥平面α，则b与α的关系是
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    下列有关命题的说法正确的是（　　）
    A、命题“若x2=1，则x=1”的否命题为：“若x2=1，则x≠1”
    B、“x=-1”是“x2-5x-6=0”的必要不充分条件
    C、命题“若x=y，则sinx=siny”的逆否命题为真命题
    D、若命题p：“?x0∈R使x02+x0+1＜0”，则￢p为假命题

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    直线y=kx+3与圆（x-2）2+（y-3）2=4相交于M、N两点，若|MN|≤2
    		3
    ，则k的取值范围是（　　）
    A、[
    		3
    ，
    		3
    ]
    B、(0，
    		3
    ]
    C、(-∞，-
    		3
    3
    ]∪[
    		3
    3
    ，+∞)
    D、[-
    		3
    3
    ，
    		3
    3
    ]

    查看答案和解析>>

    科目：高中数学 来源： 题型：

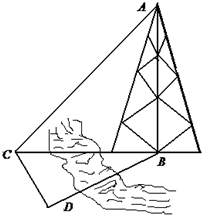    如图，测量河对岸的塔高AB时，可以选与塔底B在同一水平面内的两个测点C，D．现测得∠BCD=60°，∠DBC=45°，CD=20m，并在点C测得塔顶A的仰角为45°，求塔高AB（精确到0.1，
    		3
    =1.732）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （1）计算（0.25） 
    1
    2
    -[-2×（
    3
    7
    ）0]2×[（-2）3] 
    4
    3
    +（
    		2
    -1）-1-2 
    1
    2
    ；
    （2）解方程：lg（x+1）+lg（x-2）=lg4．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设x，y满足
    (x-2)2+(y-2)2≤1
    y≥2
    ，则
    y
    x
    的取值范围是
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在△ABC中，sinC=
    5
    13
    ，cosB=-
    4
    5
    ，则角cosA=
     
    ．

    查看答案和解析>>

    同步练习册答案