
| A. | $\frac{40}{3}$ | B. | $\frac{16}{3}$ | C. | 8 | D. | 12 |
分析 由条件利用等比数列的定义和性质,求得第1项与第2项,可得第1项与第2项的和.
解答 解:∵设这个等比数列为{an},则由题意可得a3=12,a4=18,
∴它的公比为 q=$\frac{{a}_{4}}{{3}_{3}}$=$\frac{3}{2}$,
则它的第一项为a1=$\frac{{a}_{3}}{{q}^{2}}$=$\frac{12}{\frac{9}{4}}$=$\frac{16}{3}$,第二项为a2=$\frac{{a}_{3}}{q}$=$\frac{12}{\frac{3}{2}}$=8,
则它的第1项与第2项的和为8+$\frac{16}{3}$=$\frac{40}{3}$,
故选:A.
点评 本题主要考查等比数列的定义和性质,属于基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | $\sqrt{15}$ | C. | $\sqrt{7}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
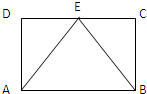 如图,矩形ABCD中,点E为边CD的中点,若在矩形ABCD内部随机抽取一个点Q,则点Q取自△ABE内部的概率等于( )
如图,矩形ABCD中,点E为边CD的中点,若在矩形ABCD内部随机抽取一个点Q,则点Q取自△ABE内部的概率等于( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 57600 | B. | 576000 | C. | 41600 | D. | 1600(22+$\sqrt{17}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com