
分析 每月付1万元,分10次付完,设每月付款数顺次组成数列{an},可得付款数{an}组成等差数列,公差d=0,01,再利用等差数列的前n项和公式,求得结论.
解答 解:购买时付了5万元,欠款10万元.每月付1万元,分10次付完,设每月付款数顺次组成数列{an},
则a1=1+10×0.01=1.1,
a2=1+(10-1)×0.01=1.09,
a3=1+(10-2)×0.01=1.08,
a4=1+(10-3)×0.01=1.07
类推,得a10=1+(10-9)×0.01=1.01,
∴5+10+(0,01+0,02+…+0,1)=15.55;
故答案为:15.55.
点评 本题主要考查等差数列的实际应用,等差数列的前n项和公式,设每月付款数顺次组成数列{an},判断付款数{an}组成等差数列,公差d=-0.5,是解题的关键,属于中档题.


 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:解答题
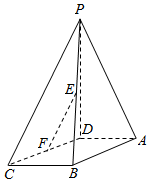 如图,在四棱锥P-ABCD中,PD⊥面ABCD,AD∥BC,CD=13,AB=12,BC=10,AD=$\frac{1}{2}$BC,点E、F分别是棱PB、边CD的中点.
如图,在四棱锥P-ABCD中,PD⊥面ABCD,AD∥BC,CD=13,AB=12,BC=10,AD=$\frac{1}{2}$BC,点E、F分别是棱PB、边CD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | 1 | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 空间三点确定一个平面 | |
| B. | 过直线外一点有且只有一条直线与已知直线垂直 | |
| C. | 如果一条直线与平面内的一条直线平行,则这条直线与平面平行 | |
| D. | 三个平面最多将可空间分成八块 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com