
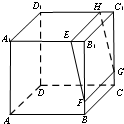
 如图,平面EFGH为长方体ABCD-A1B1C1D1的截面,E为线段A1B1上异于B1的点,F为线段BB1上异于B1的点,EH∥A1D1,则四边形EFGH的形状是( )
如图,平面EFGH为长方体ABCD-A1B1C1D1的截面,E为线段A1B1上异于B1的点,F为线段BB1上异于B1的点,EH∥A1D1,则四边形EFGH的形状是( )| A、平行四边形 | B、梯形 |
| C、菱形 | D、矩形 |


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
| a1 |
| a2 |
| a3 |
| a4 |
| a5 |
| d1 |
| d2 |
| d3 |
| d4 |
| d5 |
| ai |
| aj |
| ak |
| dr |
| ds |
| dt |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、15 | B、5 | C、10 | D、20 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、f(4)=6 |
| B、f(4)=4 |
| C、f(4)=5 |
| D、f(4)=7 |
查看答案和解析>>
科目:高中数学 来源: 题型:
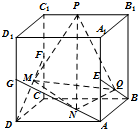 已知点E、F、G分别是正方体ABCD-A1B1C1D1的棱AA1、CC1、DD1的中点,点M、N、Q、P分别在线段DF、AG、BE、C1B1上.以M、N、Q、P为顶点的三棱锥P-MNQ的俯视图不可能是( )
已知点E、F、G分别是正方体ABCD-A1B1C1D1的棱AA1、CC1、DD1的中点,点M、N、Q、P分别在线段DF、AG、BE、C1B1上.以M、N、Q、P为顶点的三棱锥P-MNQ的俯视图不可能是( )A、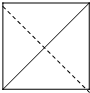 |
B、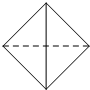 |
C、 |
D、 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| f(-1) |
| g(-1) |
| f(1) |
| g(1) |
A、
| ||
| B、3 | ||
C、
| ||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
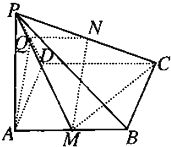 已知PA⊥平面ABCD,四边形ABCD为矩形,PA=AD,M、N分别是AB、PC的中点,求证:
已知PA⊥平面ABCD,四边形ABCD为矩形,PA=AD,M、N分别是AB、PC的中点,求证:查看答案和解析>>
科目:高中数学 来源: 题型:
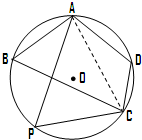 市某棚户区改造建筑用地平面示意图如图所示.经规划调研确定,棚改规划建筑用地区域是半径为R的圆面.该圆面的内接四边形ABCD是原棚户建筑用地,测量可知边界AB=AD=4万米,BC=6万米,CD=2万米.
市某棚户区改造建筑用地平面示意图如图所示.经规划调研确定,棚改规划建筑用地区域是半径为R的圆面.该圆面的内接四边形ABCD是原棚户建筑用地,测量可知边界AB=AD=4万米,BC=6万米,CD=2万米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com