
如图,已知正四棱锥S﹣ABCD的底面边长为2,高为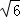 ,P为棱SC的中点.
,P为棱SC的中点.
(1)求直线AP与平面SBC所成角的正弦值;
(2)求两面角B﹣SC﹣D大小的余弦值;
(3)在正方形ABCD内是否有一点Q,使得PQ⊥平面SDC?若存在,求PQ的长;若不存在,请说明理由.
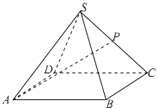
解:(1)设正方形ABCD的中心为O,如图建立空间直角坐标系,
则A(1,﹣1,0),B(1,1,0),C(﹣1,1,0),
D(﹣1,﹣1,0),S(0,0,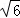 ),
),
∵P是SC的中点,∴P(﹣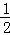 ,
,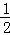 ,
,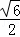 ).…(2分)
).…(2分)
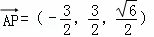 ,设平面SBC的法向量
,设平面SBC的法向量 =(x1,y1,z1),
=(x1,y1,z1),
则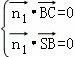 ,即
,即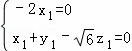 ,取
,取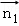 =(0,
=(0,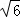 ,1),
,1),
∴cos<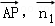 >=
>=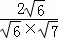 =
=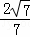 ,…(4分)
,…(4分)
故直线AP与平面SBC所成角的正弦值为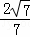 .…(6分)
.…(6分)
(2)设平面SDC的法向量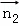 =(x2,y2,z2),则
=(x2,y2,z2),则
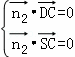 ,即
,即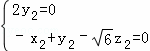 ,取
,取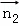 =(﹣
=(﹣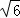 ,0,1),
,0,1),
∴cos<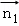 ,
,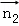 >=
>=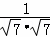 =
=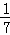 ,…(9分)
,…(9分)
又二面角B﹣SC﹣D为钝角二面角,
故二面角B﹣SC﹣D大小的余弦值为﹣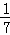 .…(11分)
.…(11分)
(3)设Q(x,y,0),则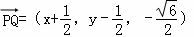 ,…(12分)
,…(12分)
若PQ⊥平面SDC,则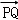 ∥
∥ ,
,
∴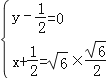 ,解得
,解得 ,…(15分)
,…(15分)
但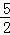 >1,点Q不在正方形ABCD内,故不存在满足条件的点Q.…(16分)
>1,点Q不在正方形ABCD内,故不存在满足条件的点Q.…(16分)


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
如图,在某个城市中,M,N两地之间有南北街道5条、东西街道4条,现要求沿图中的街道,以最短的路程从M走到N,则不同的走法共有 _________ 种.

查看答案和解析>>
科目:高中数学 来源: 题型:
班级53名同学报名参加科技、文化、生活三个学习社团,规定每人必须参加一个社团,且最多参加两个社团,在所有可能的报名方案中,设参加社团完全相同的人数的最大值为n,则n的最小值为 _________ .
查看答案和解析>>
科目:高中数学 来源: 题型:
某食品厂定期购买面粉,已知该厂每天需要面粉6吨,每吨面粉的价格为1800元,面粉的保管等其它费用为平均每吨每天3元,购面粉每次需支付运费900元.求该厂多少天购买一次面粉,才能使平均每天所支付的总费用最少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com