
 在如图所示的多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AB=CD=1,AC=$\sqrt{3}$,AD=DE=2.
在如图所示的多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AB=CD=1,AC=$\sqrt{3}$,AD=DE=2.分析 (Ⅰ)根据线面平行的判定定理即可确定F的位置
(Ⅱ)建立坐标系求出平面的法向量,利用直线和平面所成角的定义进行求解即可.
解答 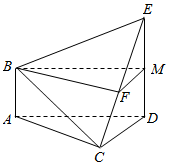 证明:(Ⅰ)取线段CE的中点F,连接BF,则BF∥平面ACD;
证明:(Ⅰ)取线段CE的中点F,连接BF,则BF∥平面ACD;
(Ⅱ)∵AB=CD=1,AC=$\sqrt{3}$,AD=DE=2
∴AD2=AC2+CD2,∴∠ACD=90°,
∴AC⊥CD,
建立以C为坐标原点,CD,CA,分别为x,y轴,过C⊥平面ACD的直线为z轴的空间直角坐标系如图:
则A(0,$\sqrt{3}$,0),D(1,0,0),B(0,$\sqrt{3}$,1),F($\frac{1}{2}$,0,1),
则$\overrightarrow{AD}$=(1,-$\sqrt{3}$,0),$\overrightarrow{AB}$=(0,0,1),$\overrightarrow{BF}$=($\frac{1}{2}$,-$\sqrt{3}$,0),
设平面ADEB的法向量为$\overrightarrow{m}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{AD}=0}\\{\overrightarrow{m}•\overrightarrow{AB}=0}\end{array}\right.$得$\left\{\begin{array}{l}{x=\sqrt{3}y}\\{z=0}\end{array}\right.$,
设y=1,则x=$\sqrt{3}$,
即$\overrightarrow{m}$=($\sqrt{3}$,1,0),
|cos<$\overrightarrow{m}$,$\overrightarrow{BF}$>|=|$\frac{\overrightarrow{m}•\overrightarrow{BF}}{|\overrightarrow{M}||\overrightarrow{BF}|}$|=$\frac{\sqrt{39}}{26}$,
即直线BF与平面ADEB所成角的正弦值sinθ=|cos<$\overrightarrow{m}$,$\overrightarrow{BF}$>|=$\frac{\sqrt{39}}{26}$.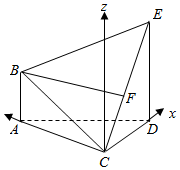
点评 本题主要考查线面平行的判断以及直线和平面所成角的求解,根据相应的判定定理以及建立坐标系,利用向量法是解决本题的关键.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
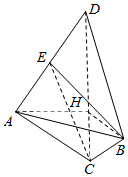 如图,在Rt△ACD中,AH⊥CD,H为垂足,CD=4,AD=2$\sqrt{3}$,∠CAD=90°,以CD为轴,将△ACD按逆时针方向旋转90°到△BCD位置,E为AD中点;
如图,在Rt△ACD中,AH⊥CD,H为垂足,CD=4,AD=2$\sqrt{3}$,∠CAD=90°,以CD为轴,将△ACD按逆时针方向旋转90°到△BCD位置,E为AD中点;查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{5}-\frac{y^2}{4}=1$ | B. | $\frac{x^2}{4}-\frac{y^2}{5}=1$ | C. | $\frac{x^2}{3}-\frac{y^2}{6}=1$ | D. | $\frac{x^2}{6}-\frac{y^2}{3}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,$\frac{7}{6}$) | B. | ($\frac{7}{6}$,+∞) | C. | [-2,$\frac{7}{6}$) | D. | (-2,-$\frac{7}{6}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 某校对高二年级进行了一次学业水平模块测试,从该年级学生中随机抽取部分学生,将他们的数学测试成绩分为6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100)加以统计,得到如图所示的频率分布直方图.已知高二年级共有学生600名,若成绩不少于80分的为优秀,据此估计,高二年级在这次测试中数学成绩优秀的学生人数为( )
某校对高二年级进行了一次学业水平模块测试,从该年级学生中随机抽取部分学生,将他们的数学测试成绩分为6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100)加以统计,得到如图所示的频率分布直方图.已知高二年级共有学生600名,若成绩不少于80分的为优秀,据此估计,高二年级在这次测试中数学成绩优秀的学生人数为( )| A. | 80 | B. | 90 | C. | 120 | D. | 150 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com