
(12分)甲、乙两人玩投篮游戏,规则如下:两人轮流投篮,每人至多投2次,甲先投,若有人投中即停止投篮,结束游戏,已知甲每次投中的概率为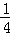 ,乙每次投中的概率为
,乙每次投中的概率为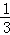 求:
求:
(Ⅰ)乙投篮次数不超过1次的概率.
(Ⅱ)记甲、乙两人投篮次数和为ξ,求ξ的分布列和数学期望.
(Ⅰ)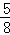 ;(Ⅱ)详见解析.
;(Ⅱ)详见解析.
【解析】
试题分析:(I)记“甲投篮投中”为事件A,“乙投篮投中”为事件B,由题设条件,“乙投篮次数不超过1次”包括三种情况:一种是甲第1次投篮投中,另一种是甲第1次投篮未投中而乙第1次投篮投中,再一种是甲、乙第1次投篮均未投中而甲第2次投篮投中,利用互斥事件的概率公式即可求解;
(II)由题意知甲、乙投篮总次数ξ的取值1,2,3,4,分别求出相应的概率,即可得到ξ的分布列与期望.
试题解析:【解析】
(I)记“甲投篮投中”为事件A,“乙投篮投中”为事件 B.
“乙投篮次数不超过1次”包括三种情况:一种是甲第1次投篮投中,另一种是甲第1次投篮未投中而乙第1次投篮投中,再一种是甲、乙第1次投篮均未投中而甲第2次投篮投中,
所求的概率是P=P(A+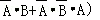
=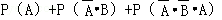 =
=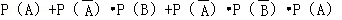
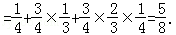
乙投篮次数不超过1次的概率为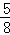 (7分)
(7分)
(2)甲、乙投篮总次数ξ的取值1,2,3,4,
P(ξ=1)=P(A)= ;
;
P(ξ=2)=P(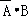 )=
)=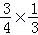 =
= ;
;
P(ξ=3)=P(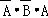 )=
)=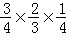 =
= ;
;
P(ξ=4)=P(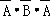 )=
)=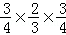 =
=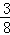 ;
;
甲、乙投篮次数总和ξ的分布列为:
ξ 1 2 3 4
P 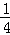
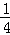
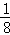
 (11分)
(11分)
甲、乙投篮总次数ξ的数学期望为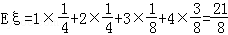 (13分)
(13分)
考点:1、互斥事件与对立事件;2、离散型随机变量的期望与方差.


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:高中数学 来源:2014-2015学年河南省濮阳市高三上学期期末摸底考试文科数学试卷(解析版) 题型:解答题
(本小题满分12分)已知数列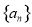 是等差数列,
是等差数列, ,
, .
.
(1)求数列 的通项公式;
的通项公式;
(2)设 ,求数列
,求数列 的前
的前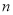 项和
项和 .
.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广西梧州、崇左两市联考高三上学期摸底文科数学试卷(解析版) 题型:解答题
已知函数f(x)=|x﹣4|﹣t,t∈R,且关于x的不等式f(x+2)≤2的解集为[﹣1,5].
(1)求t值;
(2)a,b,c均为正实数,且a+b+c=t,求证: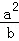 +
+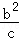 +
+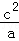 ≥1.
≥1.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广西梧州、崇左两市联考高三上学期摸底文科数学试卷(解析版) 题型:选择题
若某物体的三视图如图所示,则该物体的体积是( )
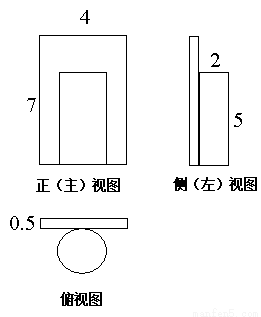
A.10+6π B.10+20π C.14+5π D.14+20π
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广西梧州、崇左两市联考高三上学期摸底理科数学试卷(解析版) 题型:解答题
已知函数f(x)=|x﹣4|﹣t,t∈R,且关于x的不等式f(x+2)≤2的解集为[﹣1,5].
(1)求t值;
(2)a,b,c均为正实数,且a+b+c=t,求证: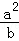 +
+ +
+ ≥1.
≥1.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广西梧州、崇左两市联考高三上学期摸底理科数学试卷(解析版) 题型:填空题
设△ABC的内角A,B,C的对边分别为a,b,c,且a=1,b=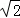 ,cosC=﹣
,cosC=﹣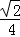 ,则sinB= _________ .
,则sinB= _________ .
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广西梧州、崇左两市联考高三上学期摸底理科数学试卷(解析版) 题型:选择题
若某物体的三视图如图所示,则该物体的体积是( )

A.10+6π B.10+20π C.14+5π D.14+20π
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省等六校高三第二次联考文科数学试卷(解析版) 题型:选择题
已知等差数列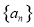 的公差
的公差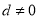 ,且
,且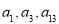 成等比数列,若
成等比数列,若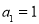 ,
, 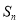 为数列
为数列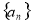 的前
的前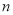 项和,则
项和,则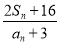 的最小值为 ( )
的最小值为 ( )
A.4 B.3 C.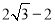 D.
D.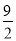
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省肇庆市小学教学评估高毕业班第二次模拟文科数学试卷(解析版) 题型:选择题
集合 由满足:对任意
由满足:对任意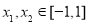 时,都有
时,都有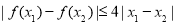 的函数
的函数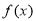 组成.对于两个函数
组成.对于两个函数 ,以下关系成立的是
,以下关系成立的是
A. B.
B.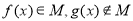
C. D.
D.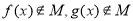
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com