【题目】已知抛物线
：
，圆
：
，直线
：
与抛物线相切于点
，与圆相切于点
.
（1）若直线的斜率
，求直线和抛物线的方程；
（2）设
为抛物线的焦点，设
，
的面积分别为
，
，若
，求
的取值范围.
【答案】（1）
：
，
：
；（2）
.
【解析】试题分析：（1）第一问，一般先设出直线的方程
，再根据直线和圆相切得到b的值. 再利用直线和抛物线方程组的判别式等于零，得到P的值. (2)第（2）问，一般利用函数的思想求
的取值范围.先要分别计算出
，
，从而得到函数
，再选择合适的方法求取值范围.
试题解析：
（1）由题设知：，且
，
由与
相切知，
到的距离
，得
，
∴：
.
将与的方程联立消
得
，
其
得
，
∴：.
综上，：，：.
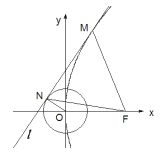
（2）不妨设
，根据对称性，得到的结论与
得到的结论相同.
此时，又知
，设
，
，
由
消
得
，
其
得
，从而解得
，
由与切于点
知到：
的距离
，得
则
，故
.
由
得
，
故
.
到：的距离为
，
∴
，
又
，
∴
.
当且仅当
即
时取等号，
与上同理可得，时亦是同上结论.
综上，的取值范围是.
科目：高中数学 来源： 题型：
【题目】基因编辑婴儿“露露”和“娜娜”出生的消息成了全球瞩目的焦点，为了解学生对基因编辑婴儿的看法，某中学随机从该校一年级学生中抽取了100人进行调查，抽取的45女生中赞成基因编辑婴儿的占
，而55名男生中有10人表示赞成基因编辑婴儿.
（1）完成
列联表，并回答能否有90%的把握认为“对基因编辑婴儿是否赞成与性别有关”？
（2）现从该校不赞成基因编辑婴儿的学生中，采用分层抽样的方法抽取7名学生，再从被抽取的7名学生中任取3人，记被抽取的3名学生女生的人数为
，求的分布列和期望.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】为了调查学生数学学习的质量情况，某校从高二年级学生（其中男生与女生的人数之比为
）中，采用分层抽样的方法抽取
名学生依期中考试的数学成绩进行统计.根据数学的分数取得了这名同学的数据，按照以下区间分为八组：
①
，②
，③
，④
，⑤
，⑥
，⑦
，⑧
得到频率分布直方图如图所示.已知抽取的学生中数学成绩少于
分的人数为
人.
（1）求的值及频率分布直方图中第④组矩形条的高度；
（2）如果把“学生数学成绩不低于
分”作为是否达标的标准，对抽取的名学生，完成下列
列联表：
据此资料，你是否认为“学生性别”与“数学成绩达标与否”有关？
（3）若从该校的高二年级学生中随机抽取
人，记这人中成绩不低于
分的学生人数为
，求的分布列、数学期望和方差
附1：“列联表
”的卡方统计量公式：
附2：卡方（
）统计量的概率分布表：
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在四棱锥P-ABCD中，平面PAD⊥底面 ABCD，侧棱PA=PD＝
，底面ABCD为直角梯形，其中BC∥AD ，AB⊥AD，AD=2AB=2BC=2,O为AD中点．
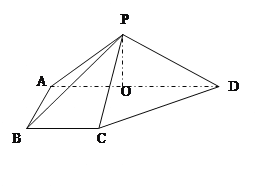
（Ⅰ）求证：PO⊥平面ABCD；
（Ⅱ）线段AD上是否存在点
，使得它到平面PCD的距离为
？若存在，求出
值；若不存在，请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某公司为了解广告投入对销售收益的影响，在若干地区各投入
万元广告费用，并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误，横轴的数据丢失，但可以确定横轴是从
开始计数的. [附：回归直线的斜率和截距的最小二乘估计公式分别为.]
（1）根据频率分布直方图计算图中各小长方形的宽度;
（2）试估计该公司投入
万元广告费用之后，对应销售收益的平均值(以各组的区间中点值代表该组的取值);
（3）该公司按照类似的研究方法,测得另外一些数据,并整理得到下表:
广告投入 | 1 | 2 | 3 | 4 | 5 |
销售收益 | 2 | 3 | 2 | 7 |
由表中的数据显示, 
与
之间存在着线性相关关系,请将（2）的结果填入空白栏,并求出
关于
的回归直线方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
