
分析 (1)由题意,利用导函数的几何含义及切点的实质建立a,b的方程,然后求解即可;
(2)由题意,若对于区间[-2,2]上任意自变量的x0,都有|f(x0)|≤c,可以转化为求函数在定义域下的最值即可得解.
解答 解:(1)f′(x)=3ax2+2bx-3.
根据题意,得$\left\{\begin{array}{l}{f(1)=-2}\\{f′(1)=0}\end{array}\right.$,
即$\left\{\begin{array}{l}{a+b-3=-2}\\{3a+2b-3=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=1}\\{b=0}\end{array}\right.$,
所以f(x)=x3-3x;
(2)令f′(x)=0,即3x2-3=0.得x=±1.
当x∈(-∞,-1)时,f′(x)>0,函数f(x)在此区间单调递增;
当x∈(-1,1)时,f′(x)<0,函数f(x)在此区间单调递减.
因为f(-1)=2,f(1)=-2,
所以当x∈[-2,2]时,f(x)max=2,f(x)min=-2.
若对于区间[-2,2]上任意自变量的x0,都有|f(x0)|≤c,所以c≥2.
所以c的最小值为2.
点评 此题重点考查了导数的几何含义及函数切点的定义,还考查了数学中重要的方程的思想,考查了数学中等价转化的思想把题意总转化为求函数在定义域下的最值.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 12 | C. | $\frac{2}{9}$ | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
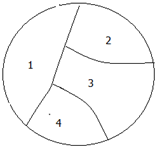 用五种不同的颜色给图中的四个区域涂色,每个区域涂一种颜色.
用五种不同的颜色给图中的四个区域涂色,每个区域涂一种颜色.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com