
分析 (1)先确定函数的定义域,再运用奇偶性的定义判断函数为奇函数;
(2)先将方程式化简,把问题你等价为$\frac{1+x}{1-x}$=e,解出即可.
解答 解:(1)∵f(x)=ln(1+x)-ln(1-x),
∴函数的定义域为:(-1,1),
且f(-x)=ln(1-x)-ln(1+x)=-f(x),
所以,f(x)为奇函数;
(2)由f(x)=ln$\frac{1+x}{1-x}$=1得,
$\frac{1+x}{1-x}$=e,解得,x=$\frac{e-1}{e+1}$,
即该方程的解为:x=$\frac{e-1}{e+1}$.
点评 本题主要考查了函数奇偶性的判断和对数方程的解法,涉及对数的运算法则和对数函数的图象与性质,属于中档题.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:高中数学 来源: 题型:填空题
 (3)请认真阅读下列程序框图:已知程序框图
(3)请认真阅读下列程序框图:已知程序框图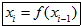 中的函数关系式为$f(x)=\frac{4x-2}{x+1}$,程序框图中的D为函数f(x)的定义域,把此程序框图中所输出的数xi组成一个数列{xn}
中的函数关系式为$f(x)=\frac{4x-2}{x+1}$,程序框图中的D为函数f(x)的定义域,把此程序框图中所输出的数xi组成一个数列{xn}查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | e | B. | $\frac{1}{e}$ | C. | 1 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{{\sqrt{5}-1}}{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com